Markov Decision Process (MDP) là một bài toán Dynamic Programming (Quy hoạch Động) được sử dụng rất nhiều trong các lĩnh vực công nghệ và đóng vai trò đặc biệt trong Reinforcement Learning (Học Tăng cường). MDP được sử dụng để mô hình hóa việc ra quyết định trong các tình huống mà kết quả là một phần ngẫu nhiên và một phần dưới sự điều khiển của người ra quyết định.
Loạt bài viết này sẽ giúp chúng ta hiểu sâu về Markov Decision Process cùng với cách xây dựng và triển khai hai thuật toán phổ biến là Policy Iteration và Value Iteration.
Khuyến nghị đọc trước Giới thiệu về Markov Chain và ứng dụng để sẵn sàng trước khi đi vào bài viết này.
Khái niệm
Markov Decision Process (Quy trình Quyết định Markov) là một quy trình quyết định trong môi trường ngẫu nhiên. Nó được mô hình hóa bằng một Markov Chain (Xích Markov) với các hành động được thực hiện bởi Agent (Tác nhân). Do đó các hành động trong tương lai sẽ không bị ảnh hưởng bởi những hành động trong quá khứ.
MDP là tiền đề của bài toán Reinforcement Learning (Học Tăng cường), chúng ta sẽ bỏ qua các khái niệm về Reinforcement Learning và cùng nhau xây dựng toàn bộ từ đầu.
Để dễ hình dung, loạt bài viết này sẽ xoay quanh tựa game Pac-Man làm ví dụ vì đây vừa là một game quen thuộc, vừa là một bài toán kinh điển trong Reinforcement Learning. MDP sẽ đóng vai trò dẫn đường cho Pac-Man đi đến đích (thức ăn) một cách nhanh nhất trong mọi trường hợp.
Các thành phần cơ bản và thiết lập game Pac-Man
Đầu tiên, chúng ta cần phải nắm vững định nghĩa của các thành phần và các quy ước kí hiệu trong MDP.
Bên cạnh đó ta cũng sẽ song song thiết lập game Pac-Man cho phần sắp tới và các bài viết sau.
Agent
Khái niệm Agent
Agent (Tác nhân) là một thực thể nằm bên trong Environment (Môi trường), đặc điểm quan trọng của Agent là nó có thể đưa ra quyết định và thực hiện các Action (Hành động) hợp lệ bên trong Environment đó.
Một Environment có thể có nhiều Agent, và tuy không được định nghĩa rõ ràng trong các bài toán, nhưng tính chất của Agent sẽ phân loại các bài toán trong Reinforcement Learning.
Các loại Agent
Agent có 2 loại là Single Agent (Đơn Tác nhân) và Multi Agent (Đa Tác nhân).
Trong Multi Agent, sẽ được chia thêm làm 2 loại là Competitive (Cạnh tranh) và Collaborative (Hợp tác).
Single Agent
Single Agent (Đơn Tác nhân) là Agent đơn lẻ, tức là chỉ có một Agent trong một Environment.
Ví dụ, thoát khỏi mê cung là một bài toán Single Agent, vì chỉ có một người chơi trong một mê cung.
Multi Agent
Multi Agent (Đa Tác nhân) là Agent đa lẻ, tức là có nhiều Agent trong một Environment.
Ví dụ về Multi Agent sẽ được đề cập ở bên dưới.
Competitive
Agent được gọi là Competitive (Cạnh tranh) khi nó sẽ phải cạnh tranh với các Agent khác trong cùng một Environment để đạt được mục đích mong muốn.
Ví dụ, cờ vua có tính chất Competitive, vì mỗi Agent sẽ phải cạnh tranh với Agent khác để giành chiến thắng.
Collaborative
Agent được gọi là Collaborative (Hợp tác) khi nó có thể hợp tác với các Agent khác trong cùng một Environment để đạt được mục đích chung.
Ví dụ, xe tự lái có tính chất Collaborative, vì các Agent sẽ phải hợp tác với nhau để tránh va chạm.
Triển khai Agent cho game Pac-Man
Agent chính là Pac-Man, thực thể có thể lựa chọn và thực hiện các Action như di chuyển lên, xuống, trái, phải đến khi đạt được mục đích.
Task
Task (Nhiệm vụ) phản ánh công việc mà Agent sẽ phải thực hiện.
Các loại Task
Task có 2 loại là Episodic (Theo tập) và Continuing (Liên tục).
Episodic
Task được gọi là Episodic (Theo tập) khi nó có Terminal State (Trạng thái Kết thúc) và Agent sẽ phải thực hiện các Action để đạt được Terminal State đó. Sau khi kết thúc, Agent sẽ bắt đầu lại từ đầu, mỗi lần như vậy được gọi là một Episode (Tập).
Ví dụ, cờ vua có tính chất Episodic, vì ta sẽ phải chơi đến khi đạt được một trạng thái kết thúc là chiến thắng hoặc đối phương đầu hàng.
Continuing
Task được gọi là Continuing (Liên tục) khi nó không có Terminal State và Agent sẽ phải thực hiện các Action liên tục cho đến khi ta chủ động dừng lại.
Ví dụ, học tập là một Continuing Task, vì lúc này sẽ không có một điểm dừng nào cả.
Triển khai Task cho game Pac-Man
Task trong game Pac-Man ta sẽ định nghĩa là đi đến thức ăn, tức là Terminal State của game là tại vị trí của thức ăn, và Pac-Man sẽ phải di chuyển đến khi vị trí này.
Environment
Khái niệm Environment
Environment (Môi trường) đóng vai trò mô tả một thế giới và các quy tắc của thế giới đó. Environment có thể bất biến hoặc thay đổi theo thời gian.
Environment có thể là một ma trận đơn giản thể hiện các vị trí với thông tin của các vật thể tương ứng trên đó. Tuy nhiên Environment cũng hoàn toàn có thể là một mô phỏng 3D phức tạp.
Các loại Environment
Environment được chia làm 2 loại, Static (Tĩnh) và Dynamic (Động).
Ngoài ra, Environment cũng có thể được chia làm 2 loại khác là Fully Observable (Quan sát Toàn Phần) và Partially Observable (Quan sát Một Phần).
Static
Environment được gọi là Static (Tĩnh) khi nó không thay đổi theo thời gian.
Ví dụ, cờ vua sẽ có Environment là Static, vì bàn cờ có các ô vuông cố định và không thể thay đổi.
Dynamic
Environment được gọi là Dynamic (Động) khi nó thay đổi theo thời gian.
Ví dụ, xe tự lái sẽ có Environment là Dynamic, vì xe tự lái sẽ di chuyển và thay đổi vị trí theo thời gian. Buộc nó phải thích nghi với những Environment mà nó chưa từng gặp.
Fully Observable
Environment được gọi là Fully Observable (Quan sát Toàn Phần) khi Agent có thể quan sát và nắm được toàn bộ thông tin của Environment. Đây là loại đơn giản nhất và thuộc loại bài toán MDP.
Ví dụ, cờ vua sẽ có Environment là Fully Observable, vì Agent có thể quan sát được toàn bộ bàn cờ và biết các quân cờ đang nằm ở đâu.
Partially Observable
Environment được gọi là Partially Observable (Quan sát Một Phần) khi Agent không thể quan sát và nắm được toàn bộ thông tin của Environment mà sẽ bị giới hạn bởi State (Trạng thái) hiện tại của Agent. Đây là loại phức tạp hơn và thuộc loại bài toán Q-Learning (Học Q) và sẽ được giới thiệu trong các bài viết sau.
Ví dụ, xe tự lái sẽ có Environment là Partially Observable, vì Agent chỉ có thể quan sát được những gì xung quanh nó, nhưng không thể quan sát được những gì xa hơn.
Triển khai Environment cho game Pac-Man
Environment là một bản đồ gồm các ô vuông, tại các vị trí đó có thể là các vật thể như: wall (tường), pit (quái), goal (thức ăn) hoặc empty (không có gì):
Đây sẽ là một ma trận với mỗi phần tử là một giá trị bất kì thuộc tập :
State
Khái niệm State
State (Trạng thái) không phải là trạng thái của Environment mà là thành phần mô tả một trạng thái có thể xảy ra của Pac-Man bên trong Environment đó. Vì thế, State chỉ có thể thay đổi khi Agent thực hiện một Action.
State thường được định nghĩa là vị trí của Agent trong Environment, nhưng nó cũng có thể là một trạng thái trừu tượng hơn như trạng thái của một đối tượng nào đó.
Để đơn giản, chúng ta sẽ mặc định các State là một tập số nguyên như bên dưới, mỗi State kí hiệu là với là số lượng State trong Environment:
Các loại State
State được chia làm 2 loại, Discrete (Rời rạc) và Continuous (Liên tục).
Discrete
State được gọi là Discrete (Rời rạc) khi các State là các số nguyên, tức là các State có thể đếm được.
Ví dụ, cờ vua sẽ có State là Discrete, vì các State là các vị trí trên bàn cờ, và các vị trí trên bàn cờ có thể đếm và xác định được.
Continuous
State được gọi là Continuous (Liên tục) khi các State là các số thực, tức là các State có thể vô hạn và có thể là bất kì giá trị nào trong khoảng cho trước.
Ví dụ, xe tự lái sẽ có State là Continuous, vì các State là các vị trí trên đường đi, các vị trí này có thể chia nhỏ đến vô hạn và có thể là bất cứ đâu trên mỗi Environment mà nó tới.
Triển khai State cho game Pac-Man
State chính là các vị trí trên bản đồ, ngay cả các vị trí là tường hay quái cũng không ngoại lệ vì ta sẽ dùng nó để xem xét các quyết định có thể xảy ra của Pac-Man.
Số State sẽ bằng số dòng nhân với số cột của , do đó ta sẽ đánh số các State từ đến tương ứng với các vị trí trên ma trận từ trái sang phải, từ trên xuống dưới:
Lúc này, ta sẽ phải định nghĩa một mapping function cho phép truy xuất tới State từ một vị trí bất kì trên bản đồ và ngược lại:
Thuật toán của chúng đơn giản như sau:
Action
Khái niệm Action
Action (Hành động) là những hành động mà Agent có thể thực hiện bên trong Environment nhằm thay đổi State để đạt được mục đính. Không phải Action cũng sẽ thực hiện được mà còn vào từng State. Và cũng không phải lúc nào Action cũng sẽ thay đổi State của Agent.
Action có thể đơn giản là tập hợp các hướng di chuyển, nhưng cũng có thể là các hành động phức tạp như thay đổi các khớp xương, trò chuyện, hay tương tác với các đối tượng khác,...
Ta cho một Action là , với là số lượng Action có thể thực hiện:
Với tính chất trên, ta sẽ định nghĩa một Mapping Function (Ánh xạ) cho phép truy xuất tới State tiếp theo dựa trên State hiện tại và Action cho trước:
Các loại Action
Action được chia làm 2 loại, Deterministic (Xác định) và Stochastic (Ngẫu nhiên).
Ngoài ra, giống với State, Action cũng được chia làm 2 loại khác là Discrete và Continuous (sẽ không cần phải nhắc lại phần này).
Deterministic
Action được gọi là Deterministic (Xác định) khi Agent thực hiện một Action nào đó thì sẽ luôn đến một State tương ứng. Tuy nhiên nó sẽ có một vài nhược điểm như hiện tượng Overfitting (Quá khớp), không thể khám phá được các State mới, hoặc có thể bị mắc kẹt.
Ví dụ khi ta thực hiện một hành động đi đến một căn phòng nào đó trong ngôi nhà hiện tại, ta sẽ luôn đến được căn phòng đó, đây được gọi là Deterministic vì tỉ lệ đến được căn phòng đó là .
Stochastic
Action được gọi là Stochastic (Ngẫu nhiên) khi Agent thực hiện một Action nào đó thì có thể đến một State khác nằm ngoài dự tính miễn là nó có thể đến được.
Một ví dụ là khi đi du lịch, với mong muốn đến một thành phố đã cho trước, ta có thể đến được thành phố đó, nhưng cũng có một tỉ lệ nhỏ là ta sẽ bị lạc đến thành phố khác hay bị mắc kẹt ở nơi hiện tại.
Triển khai Action cho game Pac-Man
Có Action có thể thực hiện tại mỗi State:
Và các Action có thể xảy ra là di chuyển sang: left (trái), right (phải), up (lên trên), down (xuống dưới):
Lí do được sắp xếp như vậy là để ta có thể dễ dàng triển khai mapping function cho phép truy xuất tới 2 hướng bên cạnh hướng đã cho:
Thuật toán tương đối đơn giản:
Giả sử Pac-Man đang có State là , sau khi đi sang phải, ta có thể biết được State mới của Pac-Man là:
Ta cũng sẽ định nghĩa rằng nếu Pac-Man đang ở biên mà thực hiện Action đi ra ngoài thì sẽ bị dội ngược lại vào trong (giữ nguyên vị trí).
Đây là lúc Stochastic phát huy tác dụng vì nếu chẳng may Policy tại đó là một Action đi ra ngoài, Pac-Man sẽ có thể trốn thoát khỏi đó sau vài lần lặp nhờ vào một Random Rate (Mức độ Ngãu nhiên) nhỏ, còn không Pac-Man sẽ mãi mãi đứng yên.
Policy
Khái niệm Policy
Policy (Kế hoạch) thể hiện một Action mà Agent nên thực hiện khi ở một State nào đó. Với một Random Rate khác , Action của Agent là Stochastic, ngược lại là Deterministic.
Policy là một mapping function cho biết tại một State nhất định, Action nào nên được thực hiện:
Policy sẽ được khởi tạo một cách ngẫu nhiên, có nghĩa là ban đầu Pac-Man sẽ đi một cách lung tung ở những lần đầu tiên, dần dần chúng ta sẽ tối ưu nó bằng các thuật toán.
Triển khai Policy cho game Pac-Man
Policy cũng là một bản đồ mà thay vì chứa các Object, các vị trí trên đó sẽ là Action mong muốn. Chỉ cần đi theo các Action đã định sẵn trên mỗi State, dù được đặt ở vị trí nào đi chăng nữa, Pac-Man vẫn sẽ luôn tìm được đường đi ngắn nhất đến thức ăn.
Random Rate
Khái niệm Random Rate
Random Rate (Mức độ Ngẫu nhiên) là một giá trị thể hiện xác suất mà Agent sẽ thực hiện một Action nằm ngoài Policy.
Đối với loại Action là Deterministic, sẽ không có gì để nói vì Agent sẽ luôn đến một State hợp lệ đã cho, do đó Random Rate sẽ bằng . Còn với loại Action là Stochastic, Random Rate sẽ là một giá trị nằm trong khoảng .
Triển khai Random Rate cho game Pac-Man
Trong ví dụ sắp tới, chúng ta sẽ cho Random Rate là theo quy tắc như sau:
- Pac-Man sẽ đi theo hướng như Policy đã chỉ định
- Pac-Man sẽ đi theo 2 hướng bên cạnh Policy.
Reward
Khái niệm Reward
Là cốt lõi của bài toán Reinforcement Learning, Reward (Phần thưởng) là một giá trị mà Agent nhận được sau khi thực hiện một Action. Tuỳ thuộc vào mỗi State mà Reward sẽ khác nhau.
Các Reward sẽ được định nghĩa từ trước, và đây là giá trị mà Agent phải dựa vào để đưa ra quyết định.
Reward, kí hiệu là , với là số lượng Reward có thể nhận được:
Vì mỗi State tương ứng với một Reward, ta có thể truy xuất một Reward từ một State bằng mapping function :
Triển khai Reward cho game Pac-Man
Chúng ta sẽ định nghĩa các các ô thức ăn có reward là , các ô quái có reward là và các ô trống có reward là (để Pac-Man tìm đường đi ngắn nhất, tránh lặp lại các hành động vô nghĩa).
Cumulative Reward
Khái niệm Cumulative Reward
Cumulative Reward (Phần thưởng Tích luỹ) là giá trị thể hiện số Reward đã tích luỹ được trong lời giải của mình. Giá trị này sẽ ảnh hưởng đến việc đánh giá một Policy là tốt hay xấu, do đó, nhiệm vụ của Agent là tìm ra lời giải sao cho giá trị này là lớn nhất.
Cucumlative Reward có thể đơn giản là tổng của các Reward, nhưng cũng có thể là một công thức phức tạp (sẽ được giới thiệu ở bài viết sau).
Gọi là tập hợp các Reward đã nhận được trong một Episode với Action đã thực hiện:
Khi đó, mapping function sẽ nhận một tập hợp gồm phần tử Reward và trả về một Cucumlative Reward nhằm phản ánh mức độ tối ưu của lời giải hiện tại:
Triển khai Cucumlative Reward cho game Pac-Man
Ta sẽ định nghĩa Cucumlative Reward là tổng của các Reward đã nhận được trên đường đi:
Transition Model
Khái niệm Transition Model
Transition Model (Mô hình Chuyển tiếp) mô tả xác suất mà một State sẽ chuyển sang State khác sau khi Agent thực hiện một Action.
Đối với loại State là Discrete, Model này sẽ được triển khai theo một Look-up Table (Bảng Tra cứu). Còn với loại State là Continuous, Model này sẽ được triển khai theo một Probability Density Function (Hàm Mật độ Xác suất).
Gọi xác suất này là tuân theo một Probability Distribution (Phân phối Xác suất) thể hiện xác suất có thể chuyển đến một State nào đó trong Environment.
Khi đó với mỗi cặp State và Action cho trước, ta có thể truy xuất được một hàm phân phối xác suất tương ứng. Đặt mapping function này là :
Triển khai Transition Model cho game Pac-Man
Cho trước một vị trí và hướng đi mong muốn, ta có thể biết được xác suất các vị trí tiếp theo mà Pac-Man sẽ đến. Tất nhiên vị trí của hướng đi mong muốn sẽ chiếm phần lớn xác suất, còn lại một phần nhỏ sẽ rơi vào các vị trí bên cạnh (tuỳ theo quy tắc đã đặt ra) và cuối cùng, các vị trí là tường, quái hay các vị trí không liền kề Pac-Man sẽ có xác suất là .
Transition Model sẽ là một 3D array trông như sau:
Hay nếu truy xuất thông qua và :
Qua đó ta có thể thấy là một Discrete Probability Distribution (Phân phối Xác suất Rời rạc), đảm bảo:
Còn nếu truy xuất chỉ thông qua , ta sẽ có một ma trận với cột là các State có thể xảy ra và hàng là các Action tương ứng:
Còn đối với việc truy xuất thông qua , mỗi Action sẽ tương ứng với một Transition Matrix (Ma trận Chuyển tiếp) như trong Markov Chain, thể hiện quá trình chuyển đổi qua lại giữa các State.
Xây dựng MDP
Chúng ta đã nắm được các khái niệm cơ bản, bây giờ quay lại bài toán Pac-Man với những giá trị từ các ví dụ đã cho ở phần trước, một bản đồ game sẽ trông như sau:
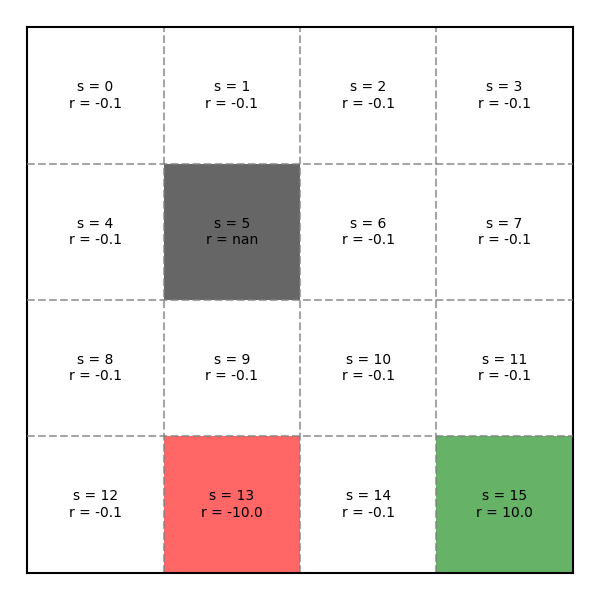
Ví dụ Environment trong game Pac-Man
Rõ ràng nhiệm vụ của chúng ta là tạo ra một Policy hợp lí. Nhưng làm thế nào để tạo Policy? Trước tiên hãy random một vài cái và nhận xét.
Policy 1
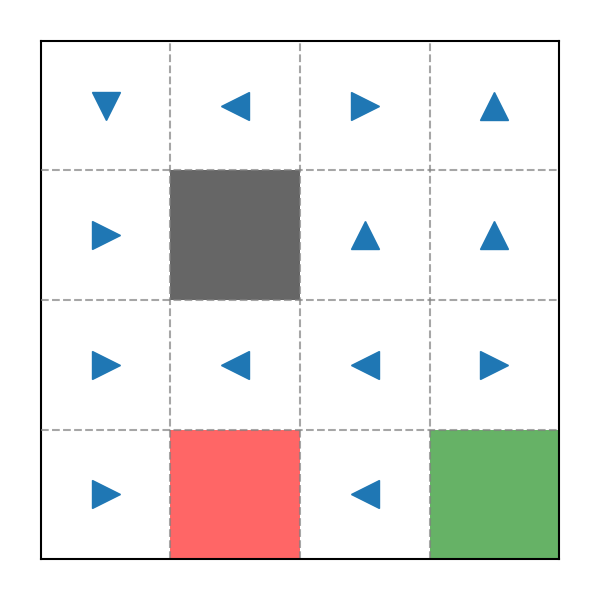
Ví dụ Policy trong game Pac-Man
Giả sử Pac-Man bắt đầu ở vị trí , nó sẽ đi sang phải , sau đó bị mắc kẹt vì không thể đi lên trên được nữa. Với lượng Random Rate đã cho (thực tế chỉ còn vì sẽ bị dội ngược lại nếu di chuyển sang phải), có thể Pac-Man sẽ quay về bên trái nhưng sau đó lại có tới đi tiếp sang phải. Rõ ràng Policy này không ổn chút nào.
Chúng ta có thể kiểm chứng bằng cách thả Pac-Man vào vị trí và cho nó di chuyển dưới dự ảnh hưởng của Policy này lần. Đối với những lần Pac-Man đến ô thức ăn màu xanh, ta sẽ kiểm tra Cucumlative Reward nhận được trong quá trình di chuyển:
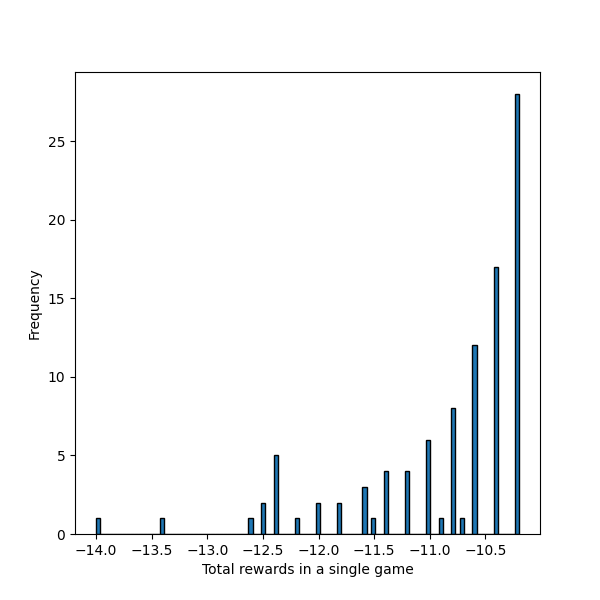
Ví dụ Policy trong game Pac-Man
Có thể thấy vì là ngẫu nhiên nên biểu đồ của chúng ta không phân bố đều. Đặc biệt là Cucumlative Reward lớn nhất chỉ có , trong số đó cũng xảy ra một vài trường hợp chỉ còn sau khi đến được ô màu xanh. Chứng tỏ Pac-Man đã đi lòng vòng khá nhiều trước khi có thể đến được đích.
Policy 2
Hãy thử tạo ngẫu nhiên một Policy khác:
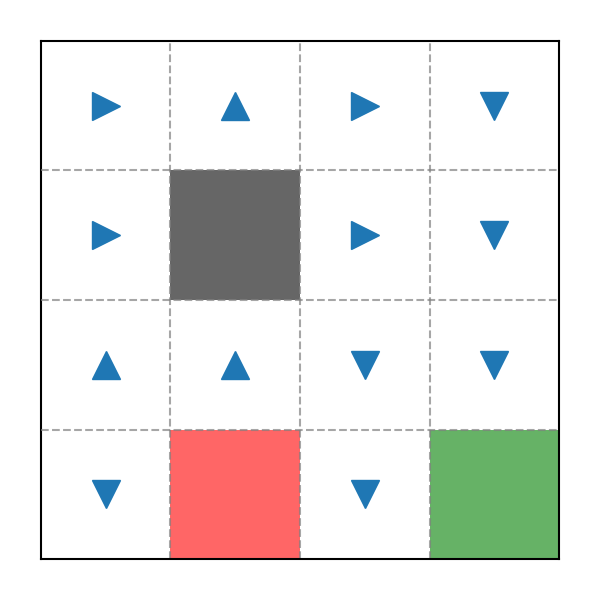
Ví dụ Policy trong game Pac-Man
Thoạt nhìn Policy này trông có vẻ ổn hơn, có một số vị trí không cần phải dựa vào Random Rate vẫn dến được đích như vị trí . Bây giờ hãy kiểm tra Cucumlative Reward thu được khi bắt đầu tại vị trí :
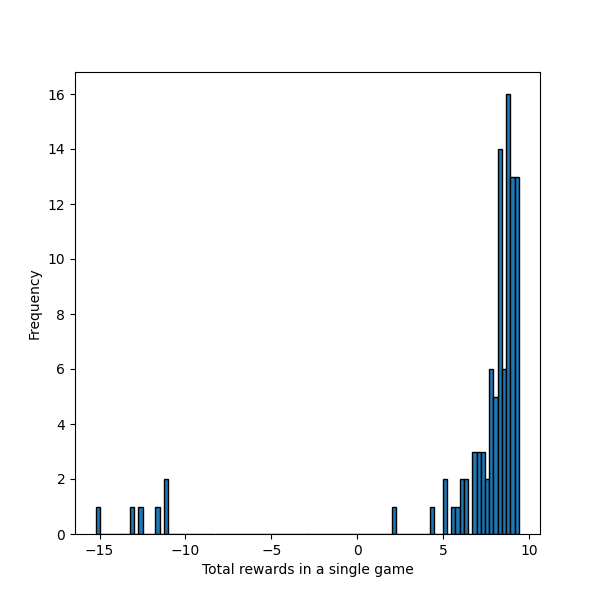
Ví dụ Policy trong game Pac-Man
Kết quả khá ấn tượng khi Cucumlative Reward cao nhất lên đến xấp xỉ , đây cũng là điểm số tối ưu nhất vì chỉ có Reward của đích đến là dương và là , chứng tỏ nó đã tốn rất ít bước di chuyển.
Tuy nhiên đây chỉ là do chúng ta mặc định bắt đầu tại , hãy thử một vị trí khác là :
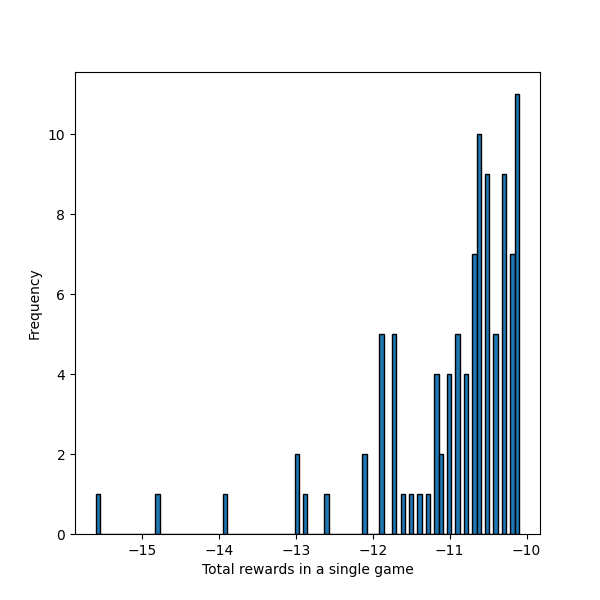
Ví dụ Policy trong game Pac-Man
Kết quả này thậm chí còn tệ hơn cả Policy 1, vậy là Policy 2 cũng không phải là một Policy tối ưu.
Policy 3
Lần này chúng ta sẽ không tạo Policy một cách ngẫu nhiên nữa mà sẽ can thiệp vào quá trình này:
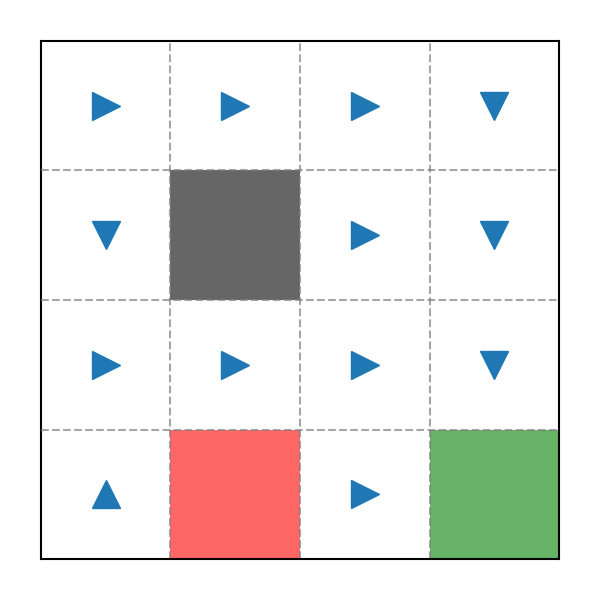
Ví dụ Policy trong game Pac-Man
Đây là một Policy "nhân tạo" đã được can thiệp, trông có vẻ rất hợp lí vì bất kì vị trí nào cũng đều dẫn đến ô màu xanh một cách ngắn nhất. Hãy kiểm tra Cucumlative Reward thu được khi bắt đầu tại vị trí :
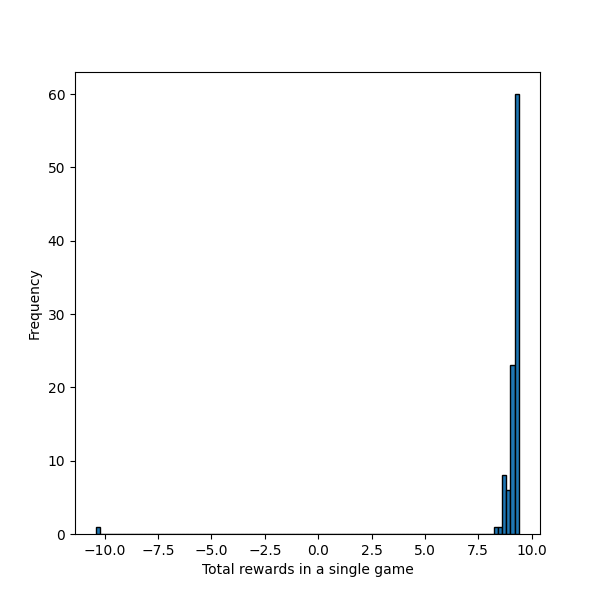
Ví dụ Policy trong game Pac-Man
Một kết quả xuất sắc, Cucumlative Reward cao nhất là , có nghĩa là nó chỉ mất điểm, tương đương với bước di chuyển để đi đến đích. Với các lần thử khác, Random Rate đã khiến nó mất thêm một ít điểm nhưng không vấn đề gì. Chúng ta không cần phải kiểm tra các vị trí khác vì kết quả cũng sẽ tương tự.
Kết luận
Số Policy khả thi trong một Environment có State với Action như trên là , có nghĩa là để tạo ngẫu nhiên ra được Policy 3, tỉ lệ sẽ là:
Tỉ lệ này tương đương với việc chọn trúng Hệ Mặt Trời của chúng ta trong giữa Dải Ngân Hà rộng lớn với hơn tỷ Ngôi Sao. Chắc chắn việc tạo ngẫu nhiên Policy là một ý tưởng tồi.
Do đó ta có 2 thuật toán chính để giúp chúng ta làm điều này, đó là Policy Iteration (Lặp theo Policy) và Value Iteration (Lặp theo Value).
Triển khai code Python
Toàn bộ code có thể xem chi tiết tại: snowyfield1906/ai-general-research/reinforcement_learning.
Thuật toán chính
Xem tại World.py.
Khởi tạo
Các mapping function
- Mapping function và :
- Mapping function và :
- Mapping function và (trả về toàn bộ thay vì mapping):
- Mapping function :
Các hàm phụ trợ
Xem tại Visualizer.py.
Kiểm thử
Xem tại test-World.py.
