Q-Learning là một thuật toán Reinforcement Learning (Học Tăng cường). Tuy không dùng đến Neural Network (Mạng Nơ-ron) nhưng thuật toán này vẫn có thể giải quyết được rất nhiều bài toán trong thực tế.
Loạt bài viết này sẽ giúp chúng ta hiểu sâu về Q-Learning cùng với cách xây dựng và triển khai hai thuật toán quan trọng là Adaptive Dynamic Programming (Quy hoạch Động Thích ứng) và Monte Carlo (Mô phỏng Monte Carlo).
Khuyến nghị đọc trước series Hiểu sâu về Markov Decision Process để sẵn sàng trước khi đi vào bài viết này.
Nhắc lại
Chúng ta đã biết cách hoạt động và các khái niệm quan trọng của Markov Decision Process trong bài viết trước. Tuy nhiên đây chỉ là một công cụ dùng để khái quát hoá bài toán Reinforcement Learning (Học Tăng cường). Thực tế, Agent thường không có khả năng biết được các thông tin quan trọng như Reward hay Transition Model.
Để hiểu đơn giản, MDP là một bài toán giúp Agent lập kế hoạch, vì lúc này Agent đã biết được các thông tin quan trọng. Trong khi đó Q-Learning bao gồm cả quá trình học để có được các thông tin này.
Q-Learning (Học Q) là một thuật toán giúp Agent có thể học được các thông tin này thông qua việc thử nhiều lần và rút ra kinh nghiệm. Để có thể triển khai được thuật toán này, chúng ta sẽ cần tìm hiểu qua hai thuật toán quan trọng là Adaptive Dynamic Programming (Quy hoạch Động Thích ứng) và Monte Carlo (Mô phỏng Monte Carlo).
Khái niệm
Adaptive Dynamic Programming (Quy hoạch Động Thích ứng) hay ADP là một thuật toán giúp Agent có thể học được các thông tin quan trọng như Reward hay Transition Model thông qua việc thử nhiều lần và rút ra kinh nghiệm. Khác với Monte Carlo (Mô phỏng Monte Carlo), ADP vẫn cần phải dựa vào Transition Model để có thể học được.
Do đó, ta gọi ADP là một thuật toán Model-based (Dựa trên Model) trong khi Monte Carlo là thuật toán Model-free (Không dựa trên Model).
Xây dựng Adaptive Dynamic Programming
Như đã nói ở trên, Q-Learning là một bài toán MDP nhưng bị khuyết đi 2 thông tin quan trọng là Reward và Transition Model. Vì vậy, chúng ta sẽ cần phải xây dựng lại 2 thông tin này thông qua việc thử nghiệm nhiều lần.
Phần này giả sử người đọc đã nắm được các kí hiệu và ví dụ ở series Hiểu sâu về Markov Decision Process.
Xây dựng Reward
Ta đặt một mapping function mô tả một bước đi của Agent. Bước đi này yêu cầu thông tin về State hiện tại và Action được thực hiện và cho biết State mới và Reward cho State cũ.
Khi đó, chúng ta có thể ước tính được Reward của một State mới (chưa từng đến) bằng cách sử dụng lại Reward của State cũ. Nói cách khác, .
Xây dựng Transition Model
Transition Model sẽ phức tạp hơn, ở bài toán MDP, Transition Model được xác định dựa trên Random Rate. Tuy nhiên, ở đây chúng ta sẽ xây dựng lại Transition Model dựa trên kinh nghiệm của Agent. Có nghĩa là Agent sẽ ưu tiên các State đã từng đạt nhiều lần trước đó thay vì mạo hiểm với các State mới. Do đó, công thức của Transition Model sẽ được xây dựng như sau:
Công thức trên có thể được hiểu là, tại State và chuẩn bị thực hiện Action , tỉ lệ Agent đạt được State sẽ là tỉ lệ mà Agent đã đạt được State đó so với các State khác khi thực hiện Action tại State trong quá khứ.
Ví dụ, với cặp State-Action :
Bằng cách lặp lại quá trình trên với tất cả các cặp State-Action, chúng ta sẽ có được một Transition Model hoàn chỉnh để phục vụ cho bước Policy Improvement.
Exploration và Exploitation
Tuy nhiên việc lặp qua toàn bộ các cặp State-Action ở bước xây dựng Transition Model như vậy sẽ rất tốn kém. Hơn nữa, bài toán này không áp dụng cho những trò chơi ảo như game Pac-Man, mà nó thường áp dụng cho các bài toán thực tế. Mà bài toán thực tế sẽ cho ra hậu quả thực tế với chi phí thực tế. Vì vậy, việc thử tất cả các trường hợp có thể xảy ra là không khả thi.
Do đó chúng ta cần phải cân bằng giữa Exploration (Khám phá) và Exploitation (Khai thác). Exploration là việc tìm kiếm và thử nghiệm các State mới, trái lại, Exploitation là việc tận dụng và cải thiện các State đã từng đạt được.
Nếu chỉ Exploration thì Agent sẽ không thể học được gì mà lại rất tốn kém, còn nếu chỉ Exploitation thì Agent sẽ mãi bị mắc kẹt tại vài State chưa phải là tối ưu.
Cách triển khai tốt nhất là chúng ta sẽ thực hiện Exploration ở những Episode đầu tiên, giúp cho Agent khám phá được nhiều State nhất có thể, sau đó thực hiện song song Exploration và Exploitation để cải thiện thông tin học được và cuối cùng là tập trung vào Exploitation.
Xây dựng Exploration và Exploitation
Để thực hiện điều này, chúng ta sẽ cho một hệ số với giá trị khởi tạo tuỳ ý (nên gần với ). Hệ số này sẽ bị giảm dần theo số Episode đã thực hiện bởi một hệ số phân rã :
Ta sẽ tạo ngẫu nhiên một số theo Uniform Distribution (Phân phối đều):
Nếu nó nằm trong phạm vi của thì Agent sẽ thực hiện Exploration, ngược lại sẽ thực hiện Exploitation:
Để dễ hình dung, chúng ta sẽ xem xét một ví dụ với trong Episode:
Có thể thấy ở những Episode đầu tiên, Agent sẽ thực hiện Exploration với xác suất rất cao, sau đó sẽ dần dần giảm xuống và tập trung vào Exploitation.
Ở lần thứ , xác suất Exploration sẽ chỉ còn và còn lại là Exploitation, một kết quả khá tốt.
Thuật toán
Chúng ta đã qua hết những thứ cần thiết để xây dựng thuật toán. Thuật toán của ADP rất đơn giản, nó gồm 3 bước:
Actuate
Đây là bước Agent lựa chọn Action để thực hiện dựa trên State hiện tại và Policy .
Quá trình này tuân theo hệ số đã xây dựng ở trên. Nếu là Exploration thì Agent sẽ lựa chọn Action ngẫu nhiên, ngược lại sẽ lựa chọn Action tốt nhất, chính là từ Policy .
Percept
Đây là bước cung cấp cho Agent những thông tin cần thiết. Bao gồm State hiện tại , Action đã chọn ở bước Actuate, State mới và Reward đã nhận được.
Reward và Transition Model sẽ được cập nhật dựa trên thông tin này bằng những công thức đã xây dựng ở trên.
Nếu là lần đầu tiên Agent đến State thì Reward và Value của State sẽ được cập nhật bằng Reward nhận được:
Policy Improvement
Khác với 2 bước trên được thực hiện ở mỗi Action, Policy Improvement chỉ được thực hiện sau khi kết thúc một Episode. Bước này sẽ cập nhật lại Policy và Value dựa trên Reward và Transition Model đã xây dựng trong Episode vừa rồi.
Quá trình cập nhật sẽ được thực hiện bằng Policy Iteration hoặc Value Iteration trong MDP.
Kết luận
Lấy ví dụ từ series trước, sau khi chạy thuật toán với 100 Episode, chúng ta có tổng Reward nhận được như sau:
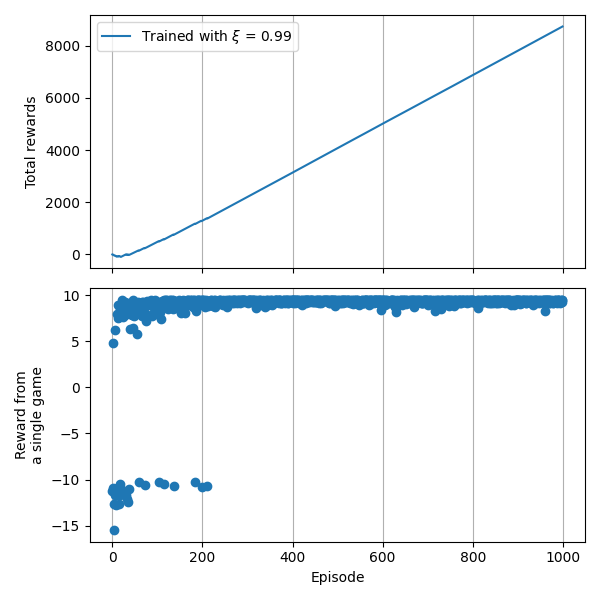
Reward nhận được sau 1000 Episode
Còn đây là tỉ lệ thắng qua mỗi Episode:
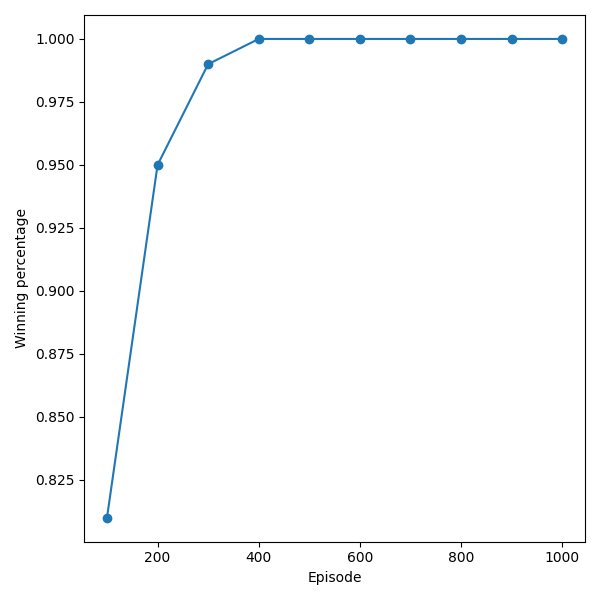
Tỉ lệ thắng nhận được sau 1000 Episode
Cuối cùng là Value tính được:
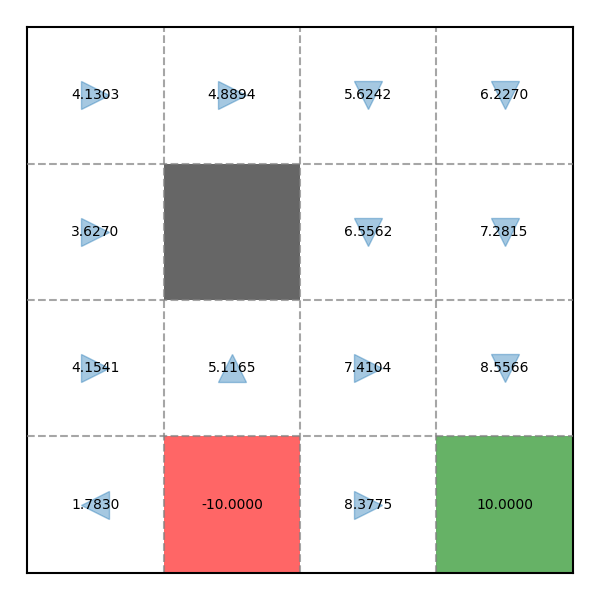
Value sau 1000 Episode
Triển khai code Python
Toàn bộ code có thể xem chi tiết tại: snowyfield1906/ai-general-research/reinforcement_learning.
Thuật toán chính
Xem tại ADPLearning.py.
Khởi tạo
Percept và Actuate
- Percept:
- Actuate:
Evaluation và Improvement
- Evaluation:
- Improvement:
Thuật toán ADP
Các hàm phụ trợ
Xem tại Visualizer.py.
Kiểm thử
Xem tại test-ADPLearning.py.
