Q-Learning là một thuật toán Reinforcement Learning (Học Tăng cường). Tuy không dùng đến Neural Network (Mạng Nơ-ron) nhưng thuật toán này vẫn có thể giải quyết được rất nhiều bài toán trong thực tế.
Loạt bài viết này sẽ giúp chúng ta hiểu sâu về Q-Learning cùng với cách xây dựng và triển khai hai thuật toán quan trọng là Adaptive Dynamic Programming (Quy hoạch Động Thích ứng) và Monte Carlo (Mô phỏng Monte Carlo).
Khuyến nghị đọc trước Phần 2 để sẵn sàng trước khi đi vào bài viết này.
Nhắc lại
Chúng ta đã biết cách hoạt động và các khái niệm quan trọng của Markov Decision Process trong series trước. Tuy nhiên đây chỉ là một công cụ dùng để khái quát hoá bài toán Reinforcement Learning (Học Tăng cường). Thực tế, Agent thường không có khả năng biết được các thông tin quan trọng như Reward hay Transition Model.
Để hiểu đơn giản, MDP là một bài toán giúp Agent lập kế hoạch, vì lúc này Agent đã biết được các thông tin quan trọng. Trong khi đó Q-Learning bao gồm cả quá trình học để có được các thông tin này.
Q-Learning (Học Q) là một thuật toán giúp Agent có thể học được các thông tin này thông qua việc thử nhiều lần và rút ra kinh nghiệm. Để có thể triển khai được thuật toán này, chúng ta sẽ cần tìm hiểu qua hai thuật toán quan trọng là Adaptive Dynamic Programming (Quy hoạch Động Thích ứng) và Monte Carlo (Mô phỏng Monte Carlo).
Khái niệm
Là một sự kết hợp giữa giữa ADP và Monte Carlo, Q-Learning sẽ có những khái niệm chung với hai thuật toán này để giải quyết những vấn đề tồn đọng trong các thuật toán trên.
Xây dựng Q-Learning
Như ta đã biết ở bài viết về Monte Carlo, chúng ta đã triển khai một khái niệm mới gọi là Q-Value được lưu trữ trong một Q-Table. Các Q-Value được cập nhật theo quy tắc Monte Carlo, tức là lấy trung bình của các C-Value (giá trị tính được sau mỗi Episode). Tuy nhiên chúng ta sẽ có một cách tiếp cận khác trong Q-Learning.
Phần này giả sử người đọc đã nắm được các kí hiệu và ví dụ ở series Hiểu sâu về Markov Decision Process.
Xây dựng Q-Value
Hãy quay lại công thức cập nhật Q-Value của Monte Carlo:
Công thức này có thể được viết lại như sau:
Trong đó:
- là Q-Table mới
- là Q-Table cũ
- là bước nhảy
- là C-Table đã tìm được tại Episode hiện tại
Nếu để ý kĩ, công thức này rất giống với Gradient Descent hay các thuật toán Optimizer khác:
Khi đó, có ý nghĩa như là , sự khác biệt giữa kiến thức cũ và mới. Trong Reinforcement Learning, này được gọi là Temporal Difference (Chênh lệch Tạm thời).
Còn , được gọi là sample-average (trung bình mẫu) có ý nghĩa như là (learning rate), thể hiện mức độ ảnh hưởng của lên . Có thể để ý rằng nếu thì , tức là chúng ta sẽ quên hết kiến thức cũ và chỉ thu nạp kiến thức mới. Ngược lại, nếu thì , tức là chúng ta sẽ không học được gì.
Xây dựng Step
Để xem xét liệu chúng ta có thể loại bỏ tham số và thay thế bằng một hằng số learning rate hay không, ta sẽ phải xem xét qua các ví dụ sau:
Cho các Q-Value ban đầu như sau:
Chúng ta sẽ thử tìm giá trị trung bình bằng cách cập nhật Q-Value theo 2 cách, một là với theo Monte Carlo và một là với .
Chúng ta sử dụng code Python sau để thực hiện việc này:
Kết quả thu được như sau:
Có thể thấy rằng sử dụng learning rate cũng cho kết quả xấp xỉ với sample-average:
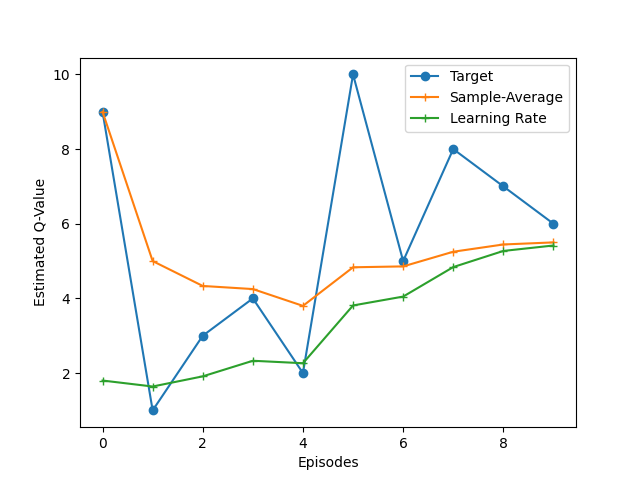
Q-Value với learning rate và sample-average
Còn đây là với :
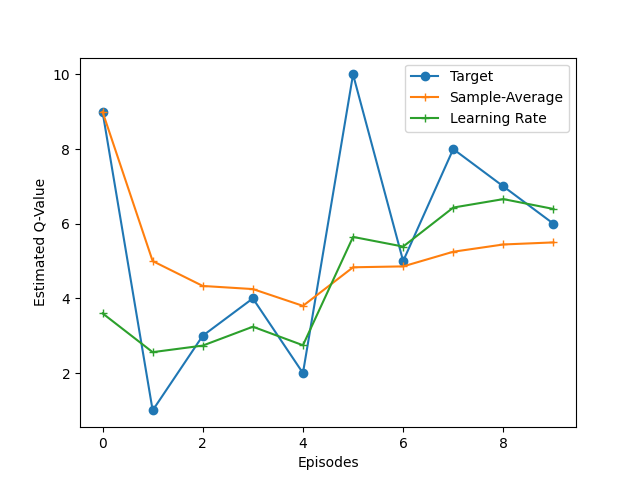
Q-Value với learning rate và sample-average
Qua đó, với một learning rate nhỏ, chúng ta có xu hướng tin vào kinh nghiệm trong quá khứ (quá trình học ít dao động hơn), còn với một learning rate lớn, chúng ta có xu hướng tin vào những gì đang xảy ra (quá trình học dao động nhiều hơn).
Trong khi đó, với việc sử dụng sample-average, các Q-Value sẽ tuân theo trung bình cộng của các C-Value một cách cực đoan.
Do đó, chúng ta có thể kiểm soát được khả năng học của Agent cũng như cho ra hiệu suất tốt hơn nhờ vào learning rate.
Loại bỏ C-Table
Như đã biết, Monte Carlo chia quá trình học thành nhiều Episode và cập nhật Q-Table sau mỗi Episode. Trong đó, mỗi Episode như là một lần học riêng biệc, dẫn đến các lần học độc lập với nhau, việc thiếu tính liên kết giữa các lần học này sẽ dẫn đến việc học không hiệu quả.
Để thực hiện việc cập nhật Q-Table một cách liên tục sau mỗi Episode, chúng ta sẽ dùng lại ví dụ so sánh Q-Value và Value ở bài viết trước:
Vì Q-Value có tính chất tương tự như Value nên chúng ta có thể sử dụng lại công thức cập nhật Value trong một Episode:
Đây sẽ là công thức thay thế cho C-Table, hay nói cách khác, đây là học được từ mỗi Episode.
Xây dựng Q-Table
Kết hợp các công thức này lại, chúng ta sẽ có công thức cập nhật Q-Value mới:
Thuật toán
Chúng ta đã qua hết những thứ cần thiết để xây dựng thuật toán. Các bước thực hiện của thuật toán Monte Carlo giống với ADP, đều gồm 3 bước dưới đây:
Actute
Đây là bước Agent lựa chọn Action để thực hiện dựa trên State hiện tại và Policy .
Bước này không có thay đổi gì với cả ADP lẫn MC. Đều dựa vào một hệ số phân rã để quyết định xem Agent sẽ thực hiện Exploration hay Exploitation. Nếu là Exploration thì Agent sẽ lựa chọn Action ngẫu nhiên, ngược lại sẽ lựa chọn Action tốt nhất, chính là từ Policy .
Percept
Đây là bước cung cấp cho Agent những thông tin cần thiết. Bao gồm State hiện tại , Action đã chọn ở bước Actuate, State mới và Reward đã nhận được.
Q-Table sẽ được cập nhật dựa trên thông tin này bằng những công thức đã xây dựng ở trên:
Thuật toán này có nghĩa là với bất kì cặp State-Action nào xuất hiện, ta sẽ dùng Q-Table hiện tại để tính Q-Value mới và dùng nó để cải thiện Q-Table.
Vì Policy dựa trên Q-Table, nên nơi nào Q-Table được cập nhật thì Policy cũng sẽ được cập nhật theo. Do đó chúng ta sẽ không cần phải thực hiện Policy Improvement sau mỗi Episode như ADP hay MC mà sẽ thêm một bước cập nhật Policy tại đây:
Decay
Trong ADP và MC, chúng ta thực hiện điều này ở bước Policy Improvement. Tuy nhiên, Policy Improvement trong Q-Learning đã được thực hiện ở bước Percept, do đó chúng ta sẽ thực hiện riêng việc giảm dần hệ số phân rã ở cuối mỗi Episode:
Kết luận
Lấy ví dụ từ series trước, sau khi chạy thuật toán với 100 Episode, chúng ta có tổng Reward nhận được như sau:
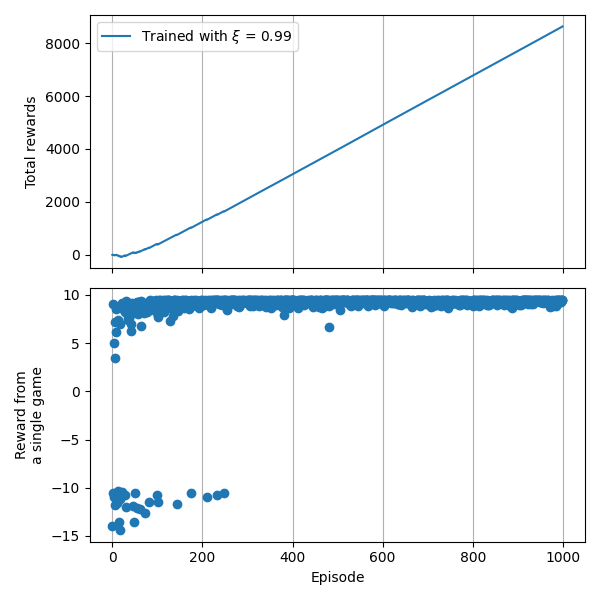
Reward nhận được sau 1000 Episode
Còn đây là tỉ lệ thắng qua mỗi Episode:
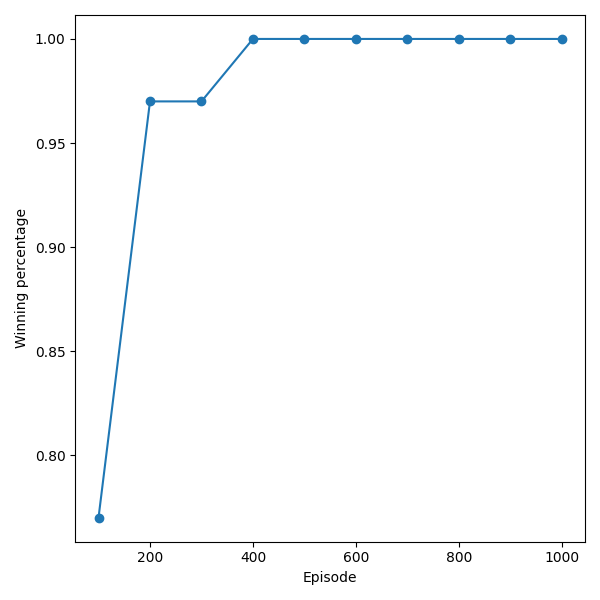
Tỉ lệ thắng nhận được sau 1000 Episode
Cuối cùng là Policy tính được:
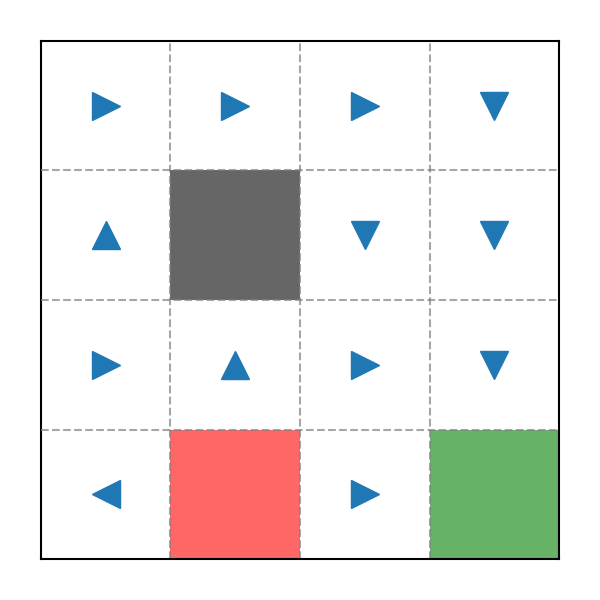
Policy sau 1000 Episode
Triển khai code Python
Toàn bộ code có thể xem chi tiết tại: snowyfield1906/ai-general-research/reinforcement_learning.
Thuật toán chính
Xem tại QLearning.py.
Khởi tạo
Percept và Actuate
- Percept:
- Actuate:
Evaluation
- Evaluation:
Thuật toán Q-Learning
Các hàm phụ trợ
Xem tại Visualizer.py.
Kiểm thử
Xem tại test-QLearning.py.
