Markov Decision Process (MDP) là một bài toán Dynamic Programming (Quy hoạch Động) được sử dụng rất nhiều trong các lĩnh vực công nghệ và đóng vai trò đặc biệt trong Reinforcement Learning (Học Tăng cường). MDP được sử dụng để mô hình hóa việc ra quyết định trong các tình huống mà kết quả là một phần ngẫu nhiên và một phần dưới sự điều khiển của người ra quyết định.
Loạt bài viết này sẽ giúp chúng ta hiểu sâu về Markov Decision Process cùng với cách xây dựng và triển khai hai thuật toán phổ biến là Policy Iteration và Value Iteration.
Khuyến nghị đọc trước Phần 1 để sẵn sàng trước khi đi vào bài viết này.
Ở phần trước chúng ta đã biết được nhiệm vụ của bài toán MDP là tìm ra một Policy π \pi π C \mathcal{C} C r r r s s s
Tuy nhiên việc tìm Policy một cách ngẫu nhiên có thể mất đến 4 16 4^{16} 4 16
Chúng ta sẽ sử dụng lại các quy ước và những gì đã triển khai ở phần trước.
Policy Iteration (Lặp theo Policy) là một thuật toán để tìm ra Policy tối ưu. Trái ngược với Value Iteration (Lặp theo Value), thuật toán này sẽ tìm ra Policy tối ưu bằng cách tạo Policy ngẫu nhiên trước, sau đó thực hiện các lần lặp để cải tiến Policy cho đến khi không còn thay đổi nào nữa.
Mỗi lần lặp sẽ thực hiện 2 bước:
Policy Evaluation (Đánh giá Policy): Tìm ra các Value mới (tối ưu hơn) từ Policy hiện tại.Policy Improvement (Cải tiến Policy): Thay đổi các Action trong Policy theo các Value mới.Value (Trị số) hay Utility (Tiện ích) là một giá trị thể hiện mức độ "tiềm năng" của một State. Value càng cao thì State đó càng gần với Terminal State (theo Policy hiện tại).
Lí do là vì sẽ có một vài State có Reward như nhau, nhưng thực tế nó không tiềm năng như nhau. Ví dụ, có 2 công ty đều có cùng lợi nhuận ở thời điểm hiện tại, nhưng công ty A kinh doanh một mặt hàng có tiềm năng trong tương lai, còn công ty B kinh doanh một mặt hàng được dự đoán là sẽ bị lỗi thời. Do đó, chúng ta cần phải tránh đầu tư (đi đến) công ty (State) B.
Chúng ta kí hiệu Value là v ∈ R v \in \mathbb{R} v ∈ R n n n V \mathcal{V} V
V : S ↦ R V ( s ) = v \begin{align} \mathcal{V} : S &\mapsto \mathbb{R} \notag \\ \mathcal{V}(s) &= v \\ \end{align} V : S V ( s ) ↦ R = v Chúng ta sẽ phải tối ưu V \mathcal{V} V
Như đã nói ở trên, tuy các vị trí là đường đi có Reward đều là − 0.1 -0.1 − 0.1
Ở phần trước, chúng ta đã quên mất một trường hợp là sẽ ra sao nếu Agent bị mắc kẹt (lặp vô hạn)? Khi đó Cumulative Reward sẽ là âm vô cùng.
Để tránh giá trị này, chúng ta sẽ sử dụng Discount Factor (Hệ số Chiết khấu) γ ∈ [ 0 , 1 ] \gamma \in [0, 1] γ ∈ [ 0 , 1 ]
C ( r = R + ) = ∑ t = 0 p − 1 γ t r t \begin{align} \mathcal{C}(r = R^+) &= \sum_{t=0}^{p-1} \gamma^t r_t \notag \\ \end{align} C ( r = R + ) = t = 0 ∑ p − 1 γ t r t Với việc nhân với γ t \gamma^t γ t p → ∞ p \to \infty p → ∞
lim p → ∞ C ( r = R + ) = lim p → ∞ ∑ t = 0 p − 1 γ t r t = r 0 + γ r 1 + γ 2 r 2 + … = 1 1 − γ arg max r t ∈ r ( r t ) \begin{align} \lim_{p \to \infty} \mathcal{C}(r = R^+) &= \lim_{p \to \infty} \sum_{t=0}^{p-1} \gamma^t r_t \notag \\ &= r_0 + \gamma r_1 + \gamma^2 r_2 + \dots \notag \\ &= \frac{1}{1 - \gamma} \arg \max_{r_t \in r} (r_t) \notag \\ \end{align} p → ∞ lim C ( r = R + ) = p → ∞ lim t = 0 ∑ p − 1 γ t r t = r 0 + γ r 1 + γ 2 r 2 + … = 1 − γ 1 arg r t ∈ r max ( r t ) Chúng ta sẽ cho Discout Factor là γ = 0.85 \gamma = 0.85 γ = 0.85
C ( r ) = ∑ t = 0 p − 1 γ t r t = r 0 + 0.85 r 1 + 0.7225 r 2 + … \begin{align} \mathcal{C}(r) &= \sum_{t=0}^{p-1} \gamma^t r_t \notag \\ &= r_0 + 0.85 r_1 + 0.7225 r_2 + \dots \notag \\ \end{align} C ( r ) = t = 0 ∑ p − 1 γ t r t = r 0 + 0.85 r 1 + 0.7225 r 2 + … Ở phần trước chúng ta chỉ đề cập đến Policy là một hàm mapping từ State sang Action, phần này chúng ta sẽ thiết lập thuật toán của Policy.
Policy và Value có mối quan hệ mật thiết với nhau, Value được tính dựa trên Policy, và Policy sẽ thay đổi theo Value. Policy ban đầu sẽ được tạo ngẫu nhiên, sau đó tính Value dựa trên Policy đó, và cuối cùng cập nhật lại Policy dựa trên Value mới.
Hành động này sẽ được lặp đi lặp lại đến khi Policy không còn thay đổi. Vì Policy sẽ cho ra Action dẫn đến State có Value cao nhất trong các State có thể đến được. Do đó thuật toán cập nhật Policy sau khi tính được Value mới đơn giản như sau:
π ( s ) = arg max a ∈ A [ V ( s ′ ) ] với s ′ = M ( s , a ) \begin{align} \mathcal{\pi}(s) = \arg \max_{a \in A} [\mathcal{V}(s')] \text{ với } s' = \mathcal{M}(s, a) \\ \end{align} π ( s ) = arg a ∈ A max [ V ( s ′ )] với s ′ = M ( s , a ) Tuy nhiên, chúng ta có một Random Rate có thể dẫn đến một State ngoài ý muốn. Vì vậy, công thức này còn phải phụ thuộc vào các State đó theo một hệ số thay vì chỉ một State duy nhất, hệ số này chính là xác suất mà Agent ngẫu nhiên đến State đó. Và đây chính là Expected Value (Giá trị Kì vọng) của State đó với Phân phối xác suất P \mathcal{P} P
π ( s ) = arg max a ∈ A E P [ V ( s ′ ) ] với s ′ = M ( s , a ) = arg max a ∈ A [ ∑ s ′ ∈ S P ( s ′ ) V ( s ′ ) ] = arg max a ∈ A [ ∑ s ′ ∈ S T ( s ′ ∣ s , a ) V ( s ′ ) ] \begin{align} \mathcal{\pi}(s) &= \arg \max_{a \in A} \mathbb{E_\mathcal{P}} \left[ \mathcal{V}(s') \right] \text{ với } s' = \mathcal{M}(s, a) \notag \\ &= \arg \max_{a \in A} \left[ \sum_{s' \in S} \mathcal{P}(s') \mathcal{V}(s') \right] \notag \\ & = \arg \max_{a \in A} \left[ \sum_{s' \in S} \mathcal{T}(s' \mid s, a) \mathcal{V}(s') \right] \\ \end{align} π ( s ) = arg a ∈ A max E P [ V ( s ′ ) ] với s ′ = M ( s , a ) = arg a ∈ A max [ s ′ ∈ S ∑ P ( s ′ ) V ( s ′ ) ] = arg a ∈ A max [ s ′ ∈ S ∑ T ( s ′ ∣ s , a ) V ( s ′ ) ] Ví dụ, cho V = { s 1 = 0.3 , s 2 = 0.1 , s 3 = − 1.5 , … } \mathcal{V} = \{s_1 = 0.3, s_2 = 0.1, s_3 = -1.5, \dots \} V = { s 1 = 0.3 , s 2 = 0.1 , s 3 = − 1.5 , … } s s s
Action a a a P = [ s 1 = 0.8 , s 2 = 0.1 , s 3 = 0.1 , … ] \mathcal{P} = [s_1 = 0.8, s_2 = 0.1, s_3 = 0.1, \dots] P = [ s 1 = 0.8 , s 2 = 0.1 , s 3 = 0.1 , … ] Action a ′ a' a ′ P ′ = [ s 1 = 0.2 , s 2 = 0.8 , s 3 = 0 , … ] \mathcal{P}' = [s_1 = 0.2, s_2 = 0.8, s_3 = 0, \dots] P ′ = [ s 1 = 0.2 , s 2 = 0.8 , s 3 = 0 , … ] Theo trực giác (cách trước đó), chúng ta sẽ cho Policy π ( s ) = a \pi(s) = a π ( s ) = a a a a s 1 s_1 s 1
Tuy nhiên a a a 10 % 10\% 10% s 3 s_3 s 3 − 1.5 -1.5 − 1.5 a ′ a' a ′ s 3 s_3 s 3
E [ V ( s ) ] = 0.8 × 0.3 + 0.1 × 0.1 + 0.1 × − 1.5 = 0.1 E [ V ( s ′ ) ] = 0.2 × 0.3 + 0.8 × 0.1 + 0 × − 1.5 = 0.14 \begin{aligned} \mathbb{E} \left[ \mathcal{V}(s) \right] &= 0.8 \times 0.3 + 0.1 \times 0.1 + 0.1 \times -1.5 \\ &= 0.1 \\ \mathbb{E} \left[ \mathcal{V}(s') \right] &= 0.2 \times 0.3 + 0.8 \times 0.1 + 0 \times -1.5 \\ &= 0.14 \\ \end{aligned} E [ V ( s ) ] E [ V ( s ′ ) ] = 0.8 × 0.3 + 0.1 × 0.1 + 0.1 × − 1.5 = 0.1 = 0.2 × 0.3 + 0.8 × 0.1 + 0 × − 1.5 = 0.14 Như vậy, a a a 0.1 0.1 0.1 a ′ a' a ′ 0.14 0.14 0.14 a ′ a' a ′ s s s
Chúng ta đã biết Value là một giá trị thể hiện mức độ "tiềm năng" của một State, Value càng cao thì State đó càng gần với Terminal State (đối với Policy hiện tại). Do đó chúng ta sẽ định nghĩa Value của một State là Cumulative Reward mà Agent có thể nhận được trong một Episode khi bắt đầu tại State đó.
Ta có công thức tính Value của một State s 0 s_0 s 0
V ( s 0 ) = ∑ t = 0 γ t R ( s t ) \begin{align} \mathcal{V}(s_0) &= \sum_{t = 0} \gamma^t \mathcal{R}(s_t) \\ \end{align} V ( s 0 ) = t = 0 ∑ γ t R ( s t ) Bằng một vài phép biến đổi đơn giản, ta có mối quan hệ giữa Value của State s 0 s_0 s 0
V ( s 0 ) = R ( s 0 ) + γ V ( s 1 ) \begin{align} \mathcal{V}(s_0) &= \mathcal{R}(s_0) + \gamma \mathcal{V}(s_1) \\ \end{align} V ( s 0 ) = R ( s 0 ) + γ V ( s 1 ) Chứng minh:
V ( s 0 ) = R ( s 0 ) + γ R ( s 1 ) + γ 2 R ( s 2 ) + … = R ( s 0 ) + γ ( R ( s 1 ) + γ R ( s 2 ) + … ) = R ( s 0 ) + γ V ( s 1 ) \begin{align} \mathcal{V}(s_0) &= \mathcal{R}(s_0) + \gamma \mathcal{R}(s_1) + \gamma^2 \mathcal{R}(s_2) + \dots \notag \\ &= \mathcal{R}(s_0) + \gamma (\mathcal{R}(s_1) + \gamma \mathcal{R}(s_2) + \dots) \notag \\ &= \mathcal{R}(s_0) + \gamma \mathcal{V}(s_1) \notag \\ \end{align} V ( s 0 ) = R ( s 0 ) + γ R ( s 1 ) + γ 2 R ( s 2 ) + … = R ( s 0 ) + γ ( R ( s 1 ) + γ R ( s 2 ) + … ) = R ( s 0 ) + γ V ( s 1 ) Để dễ hình dung, hãy xem qua hình bên dưới:
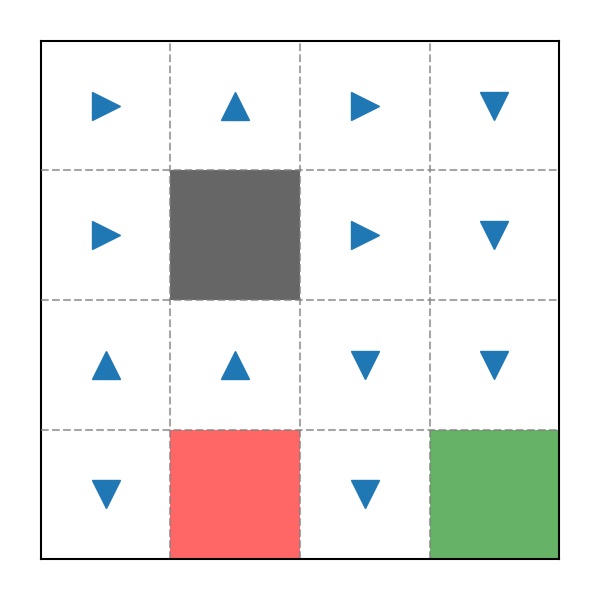
Ví dụ Policy trong game Pac-Man 2
Giả sử Pac-Man bắt đầu tại State s 0 = 2 s_0 = 2 s 0 = 2
s 0 = 2 r 0 = R ( s 0 = 2 ) = − 0.1 \begin{align} s_0 &&&= 2 \notag \\ r_0 &= \mathcal{R}(s_0 = 2) &&= -0.1 \notag \\ \end{align} s 0 r 0 = R ( s 0 = 2 ) = 2 = − 0.1 s 1 = A ( s 0 = 2 , a = right ) = 3 r 1 = R ( s 1 = 3 ) = − 0.1 \begin{align} s_1 &= \mathcal{A}(s_0 = 2, a = \text{right}) &&= 3 \notag \\ r_1 &= \mathcal{R}(s_1 = 3) &&= -0.1 \notag \\ \end{align} s 1 r 1 = A ( s 0 = 2 , a = right ) = R ( s 1 = 3 ) = 3 = − 0.1 s 2 = A ( s 1 = 3 , a = down ) = 7 r 2 = R ( s 2 = 7 ) = − 0.1 \begin{align} s_2 &= \mathcal{A}(s_1 = 3, a = \text{down}) &&= 7 \notag \\ r_2 &= \mathcal{R}(s_2 = 7) &&= -0.1 \notag \\ \end{align} s 2 r 2 = A ( s 1 = 3 , a = down ) = R ( s 2 = 7 ) = 7 = − 0.1 s 3 = A ( s 2 = 7 , a = down ) = 11 r 3 = R ( s 3 = 11 ) = − 0.1 \begin{align} s_3 &= \mathcal{A}(s_2 = 7, a = \text{down}) &&= 11 \notag \\ r_3 &= \mathcal{R}(s_3 = 11) &&= -0.1 \notag \\ \end{align} s 3 r 3 = A ( s 2 = 7 , a = down ) = R ( s 3 = 11 ) = 11 = − 0.1 Bước cuối cùng (đã đạt Terminal State s = 15 s = 15 s = 15 s 4 = A ( s 3 = 11 , a = down ) = 15 r 4 = R ( s 4 = 15 ) = + 10 \begin{align} s_4 &= \mathcal{A}(s_3 = 11, a = \text{down}) &&= 15 \notag \\ r_4 &= \mathcal{R}(s_4 = 15) &&= +10 \notag \\ \end{align} s 4 r 4 = A ( s 3 = 11 , a = down ) = R ( s 4 = 15 ) = 15 = + 10 Khi đó Value của State s 0 = 2 s_0 = 2 s 0 = 2
R + = [ − 0.1 , − 0.1 , − 0.1 , − 0.1 , + 10 ] ⟹ V ( s = 2 ) = C ( r = R + ) = ∑ t = 0 4 0.85 t r t = − 0.1 + 0.85 × − 0.1 + 0.8 5 2 × − 0.1 + … ≈ 4.901 \begin{align} &R^+ &&= [-0.1, -0.1, -0.1, -0.1, +10] \notag \\ \implies &\mathcal{V}(s = 2) &&= \mathcal{C}(r = R^+) \notag \\ &&&= \sum_{t=0}^{4} {0.85}^t r_t \notag \\ &&&= -0.1 + 0.85 \times -0.1 + 0.85^2 \times -0.1 + \ldots \notag \\ &&&\approx 4.901 \notag \\ \end{align} ⟹ R + V ( s = 2 ) = [ − 0.1 , − 0.1 , − 0.1 , − 0.1 , + 10 ] = C ( r = R + ) = t = 0 ∑ 4 0.85 t r t = − 0.1 + 0.85 × − 0.1 + 0.8 5 2 × − 0.1 + … ≈ 4.901 Tương tự, với State s 0 = 3 s_0 = 3 s 0 = 3
R + = [ − 0.1 , − 0.1 , − 0.1 , + 10 ] ⟹ V ( s = 3 ) ≈ 5.884 \begin{align} &R^+ &&= [-0.1, -0.1, -0.1, +10] \notag \\ \implies &\mathcal{V}(s = 3) &&\approx 5.884 \notag \\ \end{align} ⟹ R + V ( s = 3 ) = [ − 0.1 , − 0.1 , − 0.1 , + 10 ] ≈ 5.884 Ta có thể kiểm chứng công thức ( 4 ) (4) ( 4 ) 4.901 = − 0.1 + 0.85 × 5.884 4.901 = -0.1 + 0.85 \times 5.884 4.901 = − 0.1 + 0.85 × 5.884
Trong công thức ( 3 ) (3) ( 3 )
s = A ( s , π ( s ) ) \begin{align} s = \mathcal{A}(s, \pi(s)) \end{align} s = A ( s , π ( s )) Tuy nhiên đối với bài toán Stochastic Action, State tiếp theo có thể là một State nằm ngoài Policy theo hệ số Random Rate.
Vì thế, thay vì đặt V \mathcal{V} V V \mathcal{V} V P \mathcal{P} P
V ( s 0 ) = E P [ ∑ t γ t R ( s t ) ] = ∑ P ( s ) γ t R ( s ) \begin{align} \mathcal{V}(s_0) &= \mathbb{E}_{\mathcal{P}}\left[\sum_{t} \gamma^t \mathcal{R}(s_t) \right] \notag \\ &= \sum\mathcal{P}(s) \gamma^t \mathcal{R}(s) \\ \end{align} V ( s 0 ) = E P [ t ∑ γ t R ( s t ) ] = ∑ P ( s ) γ t R ( s ) Hay:
V ( s 0 ) = R ( s 0 ) + γ E P [ V ( s 1 ) ] = R ( s 0 ) + γ ∑ P ( s 1 ) V ( s 1 ) = R ( s 0 ) + γ ∑ T ( s 1 ∣ s 0 , π ( s 0 ) ) V ( s 1 ) \begin{align} \mathcal{V}(s_0) &= \mathcal{R}(s_0) + \gamma \mathbb{E}_{\mathcal{P}}\left[\mathcal{V}(s_1)\right] \notag \\ &= \mathcal{R}(s_0) + \gamma \sum \mathcal{P}(s_1) \mathcal{V}(s_1) \notag \\ &= \mathcal{R}(s_0) + \gamma \sum \mathcal{T}(s_1 \mid s_0, \pi(s_0)) \mathcal{V}(s_1) \\ \end{align} V ( s 0 ) = R ( s 0 ) + γ E P [ V ( s 1 ) ] = R ( s 0 ) + γ ∑ P ( s 1 ) V ( s 1 ) = R ( s 0 ) + γ ∑ T ( s 1 ∣ s 0 , π ( s 0 )) V ( s 1 ) Quay lại với ví dụ trước:
Ví dụ Policy trong game Pac-Man 2
Thay vì:
V ( 2 ) = R ( 2 ) + γ V ( 3 ) V ( 3 ) = R ( 3 ) + γ V ( 7 ) V ( 7 ) = R ( 7 ) + γ V ( 11 ) V ( 11 ) = R ( 11 ) + γ V ( 15 ) V ( 15 ) = R ( 15 ) \begin{align} \mathcal{V}(2) &= \mathcal{R}(2) + \gamma \mathcal{V}(3) \notag \\ \mathcal{V}(3) &= \mathcal{R}(3) + \gamma \mathcal{V}(7) \notag \\ \mathcal{V}(7) &= \mathcal{R}(7) + \gamma \mathcal{V}(11) \notag \\ \mathcal{V}(11) &= \mathcal{R}(11) + \gamma \mathcal{V}(15) \notag \\ \mathcal{V}(15) &= \mathcal{R}(15) \notag \\ \end{align} V ( 2 ) V ( 3 ) V ( 7 ) V ( 11 ) V ( 15 ) = R ( 2 ) + γ V ( 3 ) = R ( 3 ) + γ V ( 7 ) = R ( 7 ) + γ V ( 11 ) = R ( 11 ) + γ V ( 15 ) = R ( 15 ) Ta sẽ chuyển sang:
V ( 2 ) = R ( 2 ) + γ [ 0.8 V ( 3 ) + 0.1 V ( 2 ) + 0.1 V ( 6 ) ] V ( 3 ) = R ( 3 ) + γ [ 0.8 V ( 7 ) + 0.1 V ( 3 ) + 0.1 V ( 2 ) ] V ( 7 ) = R ( 7 ) + γ [ 0.8 V ( 11 ) + 0.1 V ( 7 ) + 0.1 V ( 6 ) ] V ( 11 ) = R ( 11 ) + γ [ 0.8 V ( 15 ) + 0.1 V ( 11 ) + 0.1 V ( 10 ) ] V ( 15 ) = R ( 15 ) \begin{align} \mathcal{V}(2) &= \mathcal{R}(2) + \gamma [0.8 \mathcal{V}(3) + 0.1 \mathcal{V}(2) + 0.1 \mathcal{V}(6)] \notag \\ \mathcal{V}(3) &= \mathcal{R}(3) + \gamma [0.8 \mathcal{V}(7) + 0.1 \mathcal{V}(3) + 0.1 \mathcal{V}(2)] \notag \\ \mathcal{V}(7) &= \mathcal{R}(7) + \gamma [0.8 \mathcal{V}(11) + 0.1 \mathcal{V}(7) + 0.1 \mathcal{V}(6)] \notag \\ \mathcal{V}(11) &= \mathcal{R}(11) + \gamma [0.8 \mathcal{V}(15) + 0.1 \mathcal{V}(11) + 0.1 \mathcal{V}(10)] \notag \\ \mathcal{V}(15) &= \mathcal{R}(15) \notag \\ \end{align} V ( 2 ) V ( 3 ) V ( 7 ) V ( 11 ) V ( 15 ) = R ( 2 ) + γ [ 0.8 V ( 3 ) + 0.1 V ( 2 ) + 0.1 V ( 6 )] = R ( 3 ) + γ [ 0.8 V ( 7 ) + 0.1 V ( 3 ) + 0.1 V ( 2 )] = R ( 7 ) + γ [ 0.8 V ( 11 ) + 0.1 V ( 7 ) + 0.1 V ( 6 )] = R ( 11 ) + γ [ 0.8 V ( 15 ) + 0.1 V ( 11 ) + 0.1 V ( 10 )] = R ( 15 ) Như đã nói ở trên, Policy Evaluation là bước tìm ra các Value mới (tối ưu hơn) từ Policy hiện tại.
Thuật toán Policy Evaluation có 2 cách triển khai chính là Xấp xỉ Value và Giải hệ phương trình tuyến tính .
Trước hết, ta sẽ mượn lại Policy ở ví dụ trên:
Ví dụ Policy trong game Pac-Man
Ta sẽ liệt kê Value của toàn bộ State:
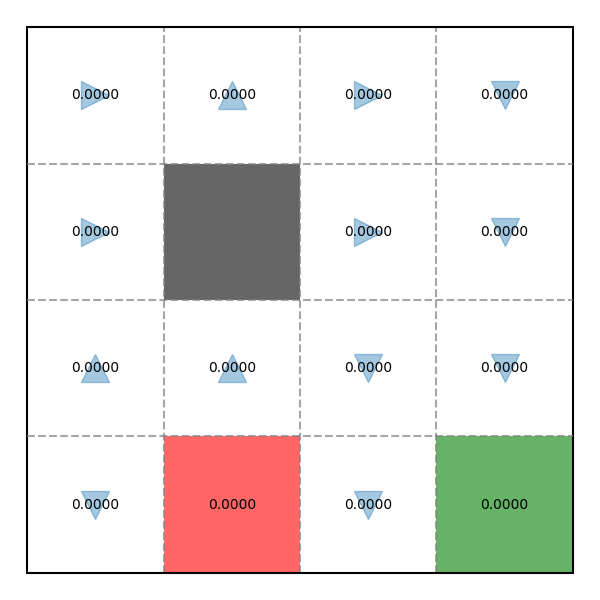
V ( 0 ) = R ( 0 ) + γ [ 0.8 V ( 1 ) + 0.1 V ( 0 ) + 0.1 V ( 4 ) ] V ( 1 ) = R ( 1 ) + γ [ 0.8 V ( 1 ) + 0.1 V ( 0 ) + 0.1 V ( 2 ) ] V ( 2 ) = R ( 2 ) + γ [ 0.8 V ( 3 ) + 0.1 V ( 2 ) + 0.1 V ( 6 ) ] V ( 3 ) = R ( 3 ) + γ [ 0.8 V ( 7 ) + 0.1 V ( 3 ) + 0.1 V ( 2 ) ] V ( 4 ) = R ( 4 ) + γ [ 0.8 V ( 4 ) + 0.1 V ( 0 ) + 0.1 V ( 8 ) ] V ( 5 ) = 0 V ( 6 ) = R ( 6 ) + γ [ 0.8 V ( 7 ) + 0.1 V ( 2 ) + 0.1 V ( 10 ) ] V ( 7 ) = R ( 7 ) + γ [ 0.8 V ( 11 ) + 0.1 V ( 7 ) + 0.1 V ( 6 ) ] V ( 8 ) = R ( 8 ) + γ [ 0.8 V ( 4 ) + 0.1 V ( 8 ) + 0.1 V ( 9 ) ] V ( 9 ) = R ( 9 ) + γ [ 0.8 V ( 9 ) + 0.1 V ( 8 ) + 0.1 V ( 10 ) ] V ( 10 ) = R ( 10 ) + γ [ 0.8 V ( 14 ) + 0.1 V ( 9 ) + 0.1 V ( 11 ) ] V ( 11 ) = R ( 11 ) + γ [ 0.8 V ( 15 ) + 0.1 V ( 11 ) + 0.1 V ( 10 ) ] V ( 12 ) = R ( 12 ) + γ [ 0.9 V ( 12 ) + 0.1 V ( 13 ) ] V ( 13 ) = R ( 13 ) + γ V ( 13 ) V ( 14 ) = R ( 14 ) + γ [ 0.8 V ( 14 ) + 0.1 V ( 13 ) + 0.1 V ( 15 ) ] V ( 15 ) = R ( 15 ) + γ V ( 15 ) \begin{align} \mathcal{V}(0) &= \mathcal{R}(0) + \gamma [0.8 \mathcal{V}(1) + 0.1 \mathcal{V}(0) + 0.1 \mathcal{V}(4)] \notag \\ \mathcal{V}(1) &= \mathcal{R}(1) + \gamma [0.8 \mathcal{V}(1) + 0.1 \mathcal{V}(0) + 0.1 \mathcal{V}(2)] \notag \\ \mathcal{V}(2) &= \mathcal{R}(2) + \gamma [0.8 \mathcal{V}(3) + 0.1 \mathcal{V}(2) + 0.1 \mathcal{V}(6)] \notag \\ \mathcal{V}(3) &= \mathcal{R}(3) + \gamma [0.8 \mathcal{V}(7) + 0.1 \mathcal{V}(3) + 0.1 \mathcal{V}(2)] \notag \\ \mathcal{V}(4) &= \mathcal{R}(4) + \gamma [0.8 \mathcal{V}(4) + 0.1 \mathcal{V}(0) + 0.1 \mathcal{V}(8)] \notag \\ \mathcal{V}(5) &= 0 \notag \\ \mathcal{V}(6) &= \mathcal{R}(6) + \gamma [0.8 \mathcal{V}(7) + 0.1 \mathcal{V}(2) + 0.1 \mathcal{V}(10)] \notag \\ \mathcal{V}(7) &= \mathcal{R}(7) + \gamma [0.8 \mathcal{V}(11) + 0.1 \mathcal{V}(7) + 0.1 \mathcal{V}(6)] \notag \\ \mathcal{V}(8) &= \mathcal{R}(8) + \gamma [0.8 \mathcal{V}(4) + 0.1 \mathcal{V}(8) + 0.1 \mathcal{V}(9)] \notag \\ \mathcal{V}(9) &= \mathcal{R}(9) + \gamma [0.8 \mathcal{V}(9) + 0.1 \mathcal{V}(8) + 0.1 \mathcal{V}(10)] \notag \\ \mathcal{V}(10) &= \mathcal{R}(10) + \gamma [0.8 \mathcal{V}(14) + 0.1 \mathcal{V}(9) + 0.1 \mathcal{V}(11)] \notag \\ \mathcal{V}(11) &= \mathcal{R}(11) + \gamma [0.8 \mathcal{V}(15) + 0.1 \mathcal{V}(11) + 0.1 \mathcal{V}(10)] \notag \\ \mathcal{V}(12) &= \mathcal{R}(12) + \gamma [0.9 \mathcal{V}(12) + 0.1 \mathcal{V}(13)] \notag \\ \mathcal{V}(13) &= \mathcal{R}(13) + \gamma\mathcal{V}(13) \notag \\ \mathcal{V}(14) &= \mathcal{R}(14) + \gamma [0.8 \mathcal{V}(14) + 0.1 \mathcal{V}(13) + 0.1 \mathcal{V}(15)] \notag \\ \mathcal{V}(15) &= \mathcal{R}(15) + \gamma\mathcal{V}(15) \\ \end{align} V ( 0 ) V ( 1 ) V ( 2 ) V ( 3 ) V ( 4 ) V ( 5 ) V ( 6 ) V ( 7 ) V ( 8 ) V ( 9 ) V ( 10 ) V ( 11 ) V ( 12 ) V ( 13 ) V ( 14 ) V ( 15 ) = R ( 0 ) + γ [ 0.8 V ( 1 ) + 0.1 V ( 0 ) + 0.1 V ( 4 )] = R ( 1 ) + γ [ 0.8 V ( 1 ) + 0.1 V ( 0 ) + 0.1 V ( 2 )] = R ( 2 ) + γ [ 0.8 V ( 3 ) + 0.1 V ( 2 ) + 0.1 V ( 6 )] = R ( 3 ) + γ [ 0.8 V ( 7 ) + 0.1 V ( 3 ) + 0.1 V ( 2 )] = R ( 4 ) + γ [ 0.8 V ( 4 ) + 0.1 V ( 0 ) + 0.1 V ( 8 )] = 0 = R ( 6 ) + γ [ 0.8 V ( 7 ) + 0.1 V ( 2 ) + 0.1 V ( 10 )] = R ( 7 ) + γ [ 0.8 V ( 11 ) + 0.1 V ( 7 ) + 0.1 V ( 6 )] = R ( 8 ) + γ [ 0.8 V ( 4 ) + 0.1 V ( 8 ) + 0.1 V ( 9 )] = R ( 9 ) + γ [ 0.8 V ( 9 ) + 0.1 V ( 8 ) + 0.1 V ( 10 )] = R ( 10 ) + γ [ 0.8 V ( 14 ) + 0.1 V ( 9 ) + 0.1 V ( 11 )] = R ( 11 ) + γ [ 0.8 V ( 15 ) + 0.1 V ( 11 ) + 0.1 V ( 10 )] = R ( 12 ) + γ [ 0.9 V ( 12 ) + 0.1 V ( 13 )] = R ( 13 ) + γ V ( 13 ) = R ( 14 ) + γ [ 0.8 V ( 14 ) + 0.1 V ( 13 ) + 0.1 V ( 15 )] = R ( 15 ) + γ V ( 15 ) Ở phương pháp này, các Value ban đầu sẽ được khởi tạo bằng 0 0 0
V ( 0 ) = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 V ( 1 ) = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 V ( 2 ) = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 V ( 3 ) = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 V ( 4 ) = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 V ( 5 ) = 0 V ( 6 ) = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 V ( 7 ) = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 V ( 8 ) = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 V ( 9 ) = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 V ( 10 ) = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 V ( 11 ) = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 V ( 12 ) = − 0.1 + 0.85 [ 0.9 × 0 + 0.1 × 0 ] = − 0.1 V ( 13 ) = − 10 + 0.85 × 0 = − 10 V ( 14 ) = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 V ( 15 ) = 10 + 0.85 × 0 = 10 \begin{align} \mathcal{V}(0) &= -0.1 + 0.85 [0.8 \times 0 + 0.1 \times 0 + 0.1 \times 0] = -0.1 \notag \\ \mathcal{V}(1) &= -0.1 + 0.85 [0.8 \times 0 + 0.1 \times 0 + 0.1 \times 0] = -0.1 \notag \\ \mathcal{V}(2) &= -0.1 + 0.85 [0.8 \times 0 + 0.1 \times 0 + 0.1 \times 0] = -0.1 \notag \\ \mathcal{V}(3) &= -0.1 + 0.85 [0.8 \times 0 + 0.1 \times 0 + 0.1 \times 0] = -0.1 \notag \\ \mathcal{V}(4) &= -0.1 + 0.85 [0.8 \times 0 + 0.1 \times 0 + 0.1 \times 0] = -0.1 \notag \\ \mathcal{V}(5) &= 0 \notag \\ \mathcal{V}(6) &= -0.1 + 0.85 [0.8 \times 0 + 0.1 \times 0 + 0.1 \times 0] = -0.1 \notag \\ \mathcal{V}(7) &= -0.1 + 0.85 [0.8 \times 0 + 0.1 \times 0 + 0.1 \times 0] = -0.1 \notag \\ \mathcal{V}(8) &= -0.1 + 0.85 [0.8 \times 0 + 0.1 \times 0 + 0.1 \times 0] = -0.1 \notag \\ \mathcal{V}(9) &= -0.1 + 0.85 [0.8 \times 0 + 0.1 \times 0 + 0.1 \times 0] = -0.1 \notag \\ \mathcal{V}(10) &= -0.1 + 0.85 [0.8 \times 0 + 0.1 \times 0 + 0.1 \times 0] = -0.1 \notag \\ \mathcal{V}(11) &= -0.1 + 0.85 [0.8 \times 0 + 0.1 \times 0 + 0.1 \times 0] = -0.1 \notag \\ \mathcal{V}(12) &= -0.1 + 0.85 [0.9 \times 0 + 0.1 \times 0] = -0.1 \notag \\ \mathcal{V}(13) &= -10 + 0.85 \times 0 = -10 \notag \\ \mathcal{V}(14) &= -0.1 + 0.85 [0.8 \times 0 + 0.1 \times 0 + 0.1 \times 0] = -0.1 \notag \\ \mathcal{V}(15) &= 10 + 0.85 \times 0 = 10 \notag \\ \end{align} V ( 0 ) V ( 1 ) V ( 2 ) V ( 3 ) V ( 4 ) V ( 5 ) V ( 6 ) V ( 7 ) V ( 8 ) V ( 9 ) V ( 10 ) V ( 11 ) V ( 12 ) V ( 13 ) V ( 14 ) V ( 15 ) = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 = 0 = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 = − 0.1 + 0.85 [ 0.9 × 0 + 0.1 × 0 ] = − 0.1 = − 10 + 0.85 × 0 = − 10 = − 0.1 + 0.85 [ 0.8 × 0 + 0.1 × 0 + 0.1 × 0 ] = − 0.1 = 10 + 0.85 × 0 = 10 Sau đó, ta lại tiếp tục thay các Value vừa rồi vào phương trình để tính toán các Value mới.
V ( 0 ) = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 V ( 1 ) = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 V ( 2 ) = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 V ( 3 ) = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 V ( 4 ) = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 V ( 5 ) = 0 V ( 6 ) = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 V ( 7 ) = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 V ( 8 ) = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 V ( 9 ) = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 V ( 10 ) = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 V ( 11 ) = − 0.1 + 0.85 [ 0.8 × 10 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = 6.68 V ( 12 ) = − 0.1 + 0.85 [ 0.9 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 V ( 13 ) = − 10 + 0.85 × − 10 = − 18.5 V ( 14 ) = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 10 + 0.1 × 10 ] = − 0.17 V ( 15 ) = 10 + 0.85 × 10 = 18.5 \begin{align} \mathcal{V}(0) &= -0.1 + 0.85 [0.8 \times -0.1 + 0.1 \times -0.1 + 0.1 \times -0.1] = -0.19 \notag \\ \mathcal{V}(1) &= -0.1 + 0.85 [0.8 \times -0.1 + 0.1 \times -0.1 + 0.1 \times -0.1] = -0.19 \notag \\ \mathcal{V}(2) &= -0.1 + 0.85 [0.8 \times -0.1 + 0.1 \times -0.1 + 0.1 \times -0.1] = -0.19 \notag \\ \mathcal{V}(3) &= -0.1 + 0.85 [0.8 \times -0.1 + 0.1 \times -0.1 + 0.1 \times -0.1] = -0.19 \notag \\ \mathcal{V}(4) &= -0.1 + 0.85 [0.8 \times -0.1 + 0.1 \times -0.1 + 0.1 \times -0.1] = -0.19 \notag \\ \mathcal{V}(5) &= 0 \notag \\ \mathcal{V}(6) &= -0.1 + 0.85 [0.8 \times -0.1 + 0.1 \times -0.1 + 0.1 \times -0.1] = -0.19 \notag \\ \mathcal{V}(7) &= -0.1 + 0.85 [0.8 \times -0.1 + 0.1 \times -0.1 + 0.1 \times -0.1] = -0.19 \notag \\ \mathcal{V}(8) &= -0.1 + 0.85 [0.8 \times -0.1 + 0.1 \times -0.1 + 0.1 \times -0.1] = -0.19 \notag \\ \mathcal{V}(9) &= -0.1 + 0.85 [0.8 \times -0.1 + 0.1 \times -0.1 + 0.1 \times -0.1] = -0.19 \notag \\ \mathcal{V}(10) &= -0.1 + 0.85 [0.8 \times -0.1 + 0.1 \times -0.1 + 0.1 \times -0.1] = -0.19 \notag \\ \mathcal{V}(11) &= -0.1 + 0.85 [0.8 \times 10 + 0.1 \times -0.1 + 0.1 \times -0.1] = 6.68 \notag \\ \mathcal{V}(12) &= -0.1 + 0.85 [0.9 \times -0.1 + 0.1 \times -0.1] = -0.19 \notag \\ \mathcal{V}(13) &= -10 + 0.85 \times -10 = -18.5 \notag \\ \mathcal{V}(14) &= -0.1 + 0.85 [0.8 \times -0.1 + 0.1 \times -10 + 0.1 \times 10] = -0.17 \notag \\ \mathcal{V}(15) &= 10 + 0.85 \times 10 = 18.5 \notag \\ \end{align} V ( 0 ) V ( 1 ) V ( 2 ) V ( 3 ) V ( 4 ) V ( 5 ) V ( 6 ) V ( 7 ) V ( 8 ) V ( 9 ) V ( 10 ) V ( 11 ) V ( 12 ) V ( 13 ) V ( 14 ) V ( 15 ) = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 = 0 = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 = − 0.1 + 0.85 [ 0.8 × 10 + 0.1 × − 0.1 + 0.1 × − 0.1 ] = 6.68 = − 0.1 + 0.85 [ 0.9 × − 0.1 + 0.1 × − 0.1 ] = − 0.19 = − 10 + 0.85 × − 10 = − 18.5 = − 0.1 + 0.85 [ 0.8 × − 0.1 + 0.1 × − 10 + 0.1 × 10 ] = − 0.17 = 10 + 0.85 × 10 = 18.5 Tiếp tục quét 1 lần nữa:
V ( 0 ) = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 V ( 1 ) = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 V ( 2 ) = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 V ( 3 ) = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 V ( 4 ) = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 V ( 5 ) = 0 V ( 6 ) = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 V ( 7 ) = − 0.1 + 0.85 [ 0.8 × 6.68 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = 4.41 V ( 8 ) = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 V ( 9 ) = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 V ( 10 ) = − 0.1 + 0.85 [ 0.8 × − 0.17 + 0.1 × − 0.19 + 0.1 × 6.68 ] = 0.34 V ( 11 ) = − 0.1 + 0.85 [ 0.8 × 18.5 + 0.1 × 6.68 + 0.1 × − 0.19 ] = 13.03 V ( 12 ) = − 0.1 + 0.85 [ 0.9 × − 0.19 + 0.1 × − 18.5 ] = − 1.82 V ( 13 ) = − 10 + 0.85 × − 18.5 = − 25.73 V ( 14 ) = − 0.1 + 0.85 [ 0.8 × − 0.17 + 0.1 × − 18.5 + 0.1 × 18.5 ] = − 0.22 V ( 15 ) = 10 + 0.85 × 18.5 = 5.73 \begin{align} \mathcal{V}(0) &= -0.1 + 0.85 [0.8 \times -0.19 + 0.1 \times -0.19 + 0.1 \times -0.19] = -0.26 \notag \\ \mathcal{V}(1) &= -0.1 + 0.85 [0.8 \times -0.19 + 0.1 \times -0.19 + 0.1 \times -0.19] = -0.26 \notag \\ \mathcal{V}(2) &= -0.1 + 0.85 [0.8 \times -0.19 + 0.1 \times -0.19 + 0.1 \times -0.19] = -0.26 \notag \\ \mathcal{V}(3) &= -0.1 + 0.85 [0.8 \times -0.19 + 0.1 \times -0.19 + 0.1 \times -0.19] = -0.26 \notag \\ \mathcal{V}(4) &= -0.1 + 0.85 [0.8 \times -0.19 + 0.1 \times -0.19 + 0.1 \times -0.19] = -0.26 \notag \\ \mathcal{V}(5) &= 0 \notag \\ \mathcal{V}(6) &= -0.1 + 0.85 [0.8 \times -0.19 + 0.1 \times -0.19 + 0.1 \times -0.19] = -0.26 \notag \\ \mathcal{V}(7) &= -0.1 + 0.85 [0.8 \times 6.68 + 0.1 \times -0.19 + 0.1 \times -0.19] = 4.41 \notag \\ \mathcal{V}(8) &= -0.1 + 0.85 [0.8 \times -0.19 + 0.1 \times -0.19 + 0.1 \times -0.19] = -0.26 \notag \\ \mathcal{V}(9) &= -0.1 + 0.85 [0.8 \times -0.19 + 0.1 \times -0.19 + 0.1 \times -0.19] = -0.26 \notag \\ \mathcal{V}(10) &= -0.1 + 0.85 [0.8 \times -0.17 + 0.1 \times -0.19 + 0.1 \times 6.68] = 0.34 \notag \\ \mathcal{V}(11) &= -0.1 + 0.85 [0.8 \times 18.5 + 0.1 \times 6.68 + 0.1 \times -0.19] = 13.03 \notag \\ \mathcal{V}(12) &= -0.1 + 0.85 [0.9 \times -0.19 + 0.1 \times -18.5] = -1.82 \notag \\ \mathcal{V}(13) &= -10 + 0.85 \times -18.5 = -25.73 \notag \\ \mathcal{V}(14) &= -0.1 + 0.85 [0.8 \times -0.17 + 0.1 \times -18.5 + 0.1 \times 18.5] = -0.22 \notag \\ \mathcal{V}(15) &= 10 + 0.85 \times 18.5 = 5.73 \notag \\ \end{align} V ( 0 ) V ( 1 ) V ( 2 ) V ( 3 ) V ( 4 ) V ( 5 ) V ( 6 ) V ( 7 ) V ( 8 ) V ( 9 ) V ( 10 ) V ( 11 ) V ( 12 ) V ( 13 ) V ( 14 ) V ( 15 ) = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 = 0 = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 = − 0.1 + 0.85 [ 0.8 × 6.68 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = 4.41 = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 = − 0.1 + 0.85 [ 0.8 × − 0.19 + 0.1 × − 0.19 + 0.1 × − 0.19 ] = − 0.26 = − 0.1 + 0.85 [ 0.8 × − 0.17 + 0.1 × − 0.19 + 0.1 × 6.68 ] = 0.34 = − 0.1 + 0.85 [ 0.8 × 18.5 + 0.1 × 6.68 + 0.1 × − 0.19 ] = 13.03 = − 0.1 + 0.85 [ 0.9 × − 0.19 + 0.1 × − 18.5 ] = − 1.82 = − 10 + 0.85 × − 18.5 = − 25.73 = − 0.1 + 0.85 [ 0.8 × − 0.17 + 0.1 × − 18.5 + 0.1 × 18.5 ] = − 0.22 = 10 + 0.85 × 18.5 = 5.73 Như vậy, sau mỗi lần quét, các Value sẽ hội tụ đến một "điểm tới hạn". Chúng ta có thể đặt một giá trị delta \text{delta} delta delta ≤ ϵ \text{delta} \leq \epsilon delta ≤ ϵ ϵ \epsilon ϵ 1 0 − 3 10^{-3} 1 0 − 3
Chúng ta đã biết R \mathcal{R} R γ \gamma γ
Để dễ dàng tính toán, ta sẽ chuyển hệ phương trình ( 8 ) (8) ( 8 ) A x = b \mathbf{A} \mathbf{x} = \mathbf{b} Ax = b
Trước hết, đặt P \mathbf{P} P 16 × 16 16 \times 16 16 × 16
s = [ s 0 , s 1 , s 2 , … , s 15 ] = [ 0 , 1 , 2 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 12 , 13 , 14 , 15 ] π = [ π ( s 0 ) , π ( s 1 ) , π ( s 2 ) , … , π ( s 15 ) ] = [ 2 , 1 , 2 , 3 , 2 , NaN , 2 , 3 , 1 , 1 , 3 , 3 , 3 , NaN , 3 , NaN ] P = T ( s = s i , a = π ( s i ) ) ∀ s i ∈ S = [ 0.1 0.8 0 0 0.1 0 0 0 0 0 0 0 0 0 0 0 0 0.1 0.8 0 0 0.1 0 0 0 0 0 0 0 0 0 0 0 0 0.1 0.8 0 0 0.1 0 0 0 0 0 0 0 0 0 0 0 0.1 0.1 0 0 0 0.8 0 0 0 0 0 0 0 0 0.8 0 0 0 0.1 0.1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0.1 0 0 0 0 0.8 0 0 0.1 0 0 0 0 0 0 0 0 0 0 0 0.1 0.1 0 0 0 0.8 0 0 0 0 0 0 0 0 0.1 0 0 0 0 0.8 0 0 0.1 0 0 0 0 0 0 0 0 0.1 0 0 0 0 0.8 0 0 0.1 0 0 0 0 0 0 0 0 0.1 0 0 0 0 0.8 0 0 0.1 0 0 0 0 0 0 0 0 0 0 0 0.1 0.1 0 0 0 0.8 0 0 0 0 0 0 0 0 0.8 0 0 0 0.1 0.1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0.1 0 0 0 0.1 0.8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 ] \begin{align} \mathbf{s} &= [s_0, s_1, s_2, \dots, s_{15}] \notag \\ &= [0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15] \notag \\ \mathbf{\pi} &= [\pi(s_0), \pi(s_1), \pi(s_2), \dots, \pi(s_{15})] \notag \\ &= [2, 1, 2, 3, 2, \text{NaN}, 2, 3, 1, 1, 3, 3, 3, \text{NaN}, 3, \text{NaN}] \notag \\ \mathbf{P} &= \mathcal{T}(s = s_i, a = \pi(s_i)) \quad \forall s_i \in S \notag \\ &= \begin{bmatrix} 0.1 & 0.8 & 0 & 0 & 0.1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0.1 & 0.8 & 0 & 0 & 0.1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0.1 & 0.8 & 0 & 0 & 0.1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0.1 & 0.1 & 0 & 0 & 0 & 0.8 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0.8 & 0 & 0 & 0 & 0.1 & 0.1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0.1 & 0 & 0 & 0 & 0 & 0.8 & 0 & 0 & 0.1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0.1 & 0.1 & 0 & 0 & 0 & 0.8 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0.1 & 0 & 0 & 0 & 0 & 0.8 & 0 & 0 & 0.1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0.1 & 0 & 0 & 0 & 0 & 0.8 & 0 & 0 & 0.1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0.1 & 0 & 0 & 0 & 0 & 0.8 & 0 & 0 & 0.1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0.1 & 0.1 & 0 & 0 & 0 & 0.8 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0.8 & 0 & 0 & 0 & 0.1 & 0.1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0.1 & 0 & 0 & 0 & 0.1 & 0.8 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} \notag \\ \end{align} s π P = [ s 0 , s 1 , s 2 , … , s 15 ] = [ 0 , 1 , 2 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 12 , 13 , 14 , 15 ] = [ π ( s 0 ) , π ( s 1 ) , π ( s 2 ) , … , π ( s 15 )] = [ 2 , 1 , 2 , 3 , 2 , NaN , 2 , 3 , 1 , 1 , 3 , 3 , 3 , NaN , 3 , NaN ] = T ( s = s i , a = π ( s i )) ∀ s i ∈ S = 0.1 0 0 0 0.8 0 0 0 0 0 0 0 0 0 0 0 0.8 0.1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.8 0.1 0.1 0 0 0.1 0 0 0 0 0 0 0 0 0 0 0 0.8 0.1 0 0 0 0 0 0 0 0 0 0 0 0 0.1 0 0 0 0.1 0 0 0 0.1 0 0 0 0 0 0 0 0 0.1 0 0 0.1 1 0 0 0 0.1 0 0 0 0 0 0 0 0 0.1 0 0 0 0 0.1 0 0 0.1 0 0 0 0 0 0 0 0 0.8 0 0 0.8 0.1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.8 0 0 0 0 0 0 0 0 0 0 0 0.8 0 0 0 0 0 0 0 0 0 0 0 0 0 0.1 0 0 0.8 0 0.1 0 0 0.1 0 0 0 0 0 0 0 0 0.8 0 0 0.8 0.1 0 0 0 0 0 0 0 0 0 0 0 0 0.1 0 0 0 0.1 0 0 0 0 0 0 0 0 0 0 0 0 0.1 0 0 0.1 1 0 0 0 0 0 0 0 0 0 0 0 0 0.1 0 0 0 0.1 0 0 0 0 0 0 0 0 0 0 0 0 0.8 0 0 0.8 1 R \mathbf{R} R V \mathbf{V} V 16 16 16
R = [ R ( s 0 ) , R ( s 1 ) , R ( s 2 ) , … , R ( s 15 ) ] = [ − 0.1 , − 0.1 , − 0.1 , − 0.1 , − 0.1 , 0 , − 0.1 , − 0.1 , − 0.1 , − 0.1 , − 0.1 , − 0.1 , − 0.1 , − 10 , − 0.1 , 10 ] V = [ V ( s 0 ) , V ( s 1 ) , V ( s 2 ) , … , V ( s 15 ) ] \begin{align} \mathbf{R} &= [\mathcal{R}(s_0), \mathcal{R}(s_1), \mathcal{R}(s_2), \dots, \mathcal{R}(s_{15})] \notag \\ &= [-0.1, -0.1, -0.1, -0.1, -0.1, 0, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -10, -0.1, 10] \notag \\ \mathbf{V} &= [\mathcal{V}(s_0), \mathcal{V}(s_1), \mathcal{V}(s_2), \dots, \mathcal{V}(s_{15})] \notag \\ \end{align} R V = [ R ( s 0 ) , R ( s 1 ) , R ( s 2 ) , … , R ( s 15 )] = [ − 0.1 , − 0.1 , − 0.1 , − 0.1 , − 0.1 , 0 , − 0.1 , − 0.1 , − 0.1 , − 0.1 , − 0.1 , − 0.1 , − 0.1 , − 10 , − 0.1 , 10 ] = [ V ( s 0 ) , V ( s 1 ) , V ( s 2 ) , … , V ( s 15 )] Khi đó:
A = I 16 − γ P b = R x = V \begin{align} \mathbf{A} &= \mathbf{I}_{16} - \gamma \mathbf{P} \notag \\ \mathbf{b} &= \mathbf{R} \notag \\ \mathbf{x} &= \mathbf{V} \notag \\ \end{align} A b x = I 16 − γ P = R = V Lúc này, ta có thể dễ dàng tìm được x \mathbf{x} x
A x = b ⟹ A − 1 A x = A − 1 b ⟹ x = A − 1 b ⟹ V = ( I 16 − γ P ) − 1 R \begin{align} \mathbf{A} \mathbf{x} &= \mathbf{b} \notag \\ \implies \mathbf{A}^{-1} \mathbf{A} \mathbf{x} &= \mathbf{A}^{-1} \mathbf{b} \notag \\ \implies \mathbf{x} &= \mathbf{A}^{-1} \mathbf{b} \notag \\ \implies \mathbf{V} &= (\mathbf{I}_{16} - \gamma \mathbf{P})^{-1} \mathbf{R} \notag \\ \end{align} Ax ⟹ A − 1 Ax ⟹ x ⟹ V = b = A − 1 b = A − 1 b = ( I 16 − γ P ) − 1 R Kết quả của cả 2 cách trên là:
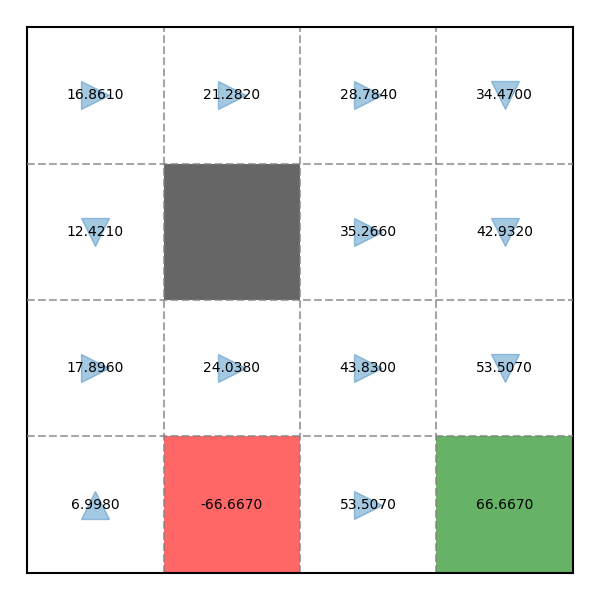
V = [ 16.861 , 21.282 , 28.784 , 34.470 , 12.421 , 0 , 35.266 , 42.932 , 17.896 , 24.038 , 43.830 , 53.507 , 6.998 , − 66.667 , 53.507 , 66.667 ] \begin{align} \mathbf{V} &= [16.861, 21.282, 28.784, 34.470, 12.421, 0, 35.266, 42.932, 17.896, 24.038, 43.830, 53.507, 6.998, -66.667, 53.507, 66.667] \end{align} V = [ 16.861 , 21.282 , 28.784 , 34.470 , 12.421 , 0 , 35.266 , 42.932 , 17.896 , 24.038 , 43.830 , 53.507 , 6.998 , − 66.667 , 53.507 , 66.667 ] Kiểm tra phép tính tại đây: Matrix Calculator
Sau khi tìm được Value mới, ta sẽ cập nhật Policy hiện tại bằng cách chọn Action có Value lớn nhất cho mỗi State theo công thức ( 2 ) (2) ( 2 )
Ví dụ Evaluation trong trong game Pac-Man
Ví dụ Improvement trong trong game Pac-Man
Kết quả khá khả qua khi sau lần Policy Improvement đầu tiên, Policy đã ở trạng thái tối ưu rồi.
Tuy nhiên, trong thực tế, chúng ta cần phải lặp lại Policy Evaluation và Policy Improvement nhiều lần cho đến khi Policy không thay đổi nữa.
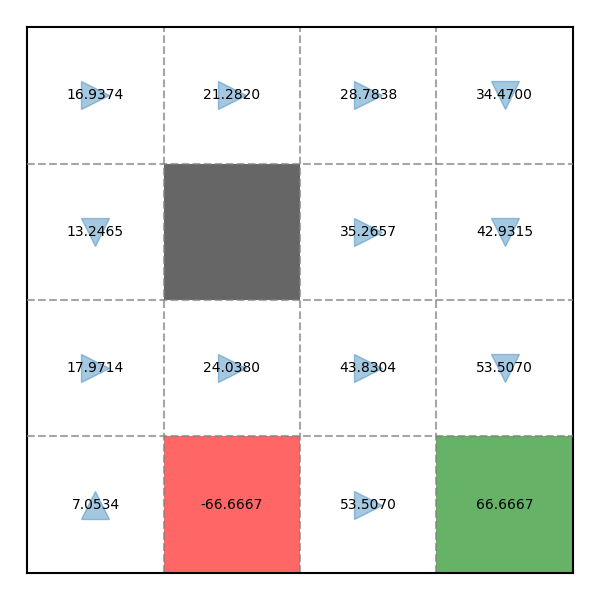
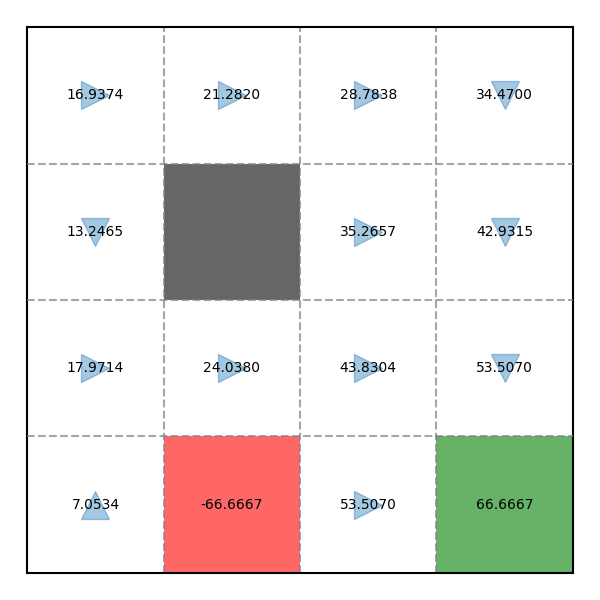
Hãy thử chạy Policy Evaluation lần 2 dựa trên kết quả của Policy Evaluation và Policy Improvement lần trước:
V = [ 16.937 , 21.282 , 28.784 , 34.47 , 13.246 , 0 , 35.266 , 42.932 , 17.971 , 24.038 , 43.83 , 53.507 , 7.053 , − 66.667 , 53.507 , 66.667 ] \begin{align} \mathbf{V} &= [16.937, 21.282, 28.784, 34.47, 13.246, 0, 35.266, 42.932, 17.971, 24.038, 43.83, 53.507, 7.053, -66.667, 53.507, 66.667] \notag \\ \end{align} V = [ 16.937 , 21.282 , 28.784 , 34.47 , 13.246 , 0 , 35.266 , 42.932 , 17.971 , 24.038 , 43.83 , 53.507 , 7.053 , − 66.667 , 53.507 , 66.667 ] Ta có kết quả sau:
Ví dụ Evaluation trong game Pac-Man
Vì Policy sau lần Improvement thứ 2 không có sự thay đổi nào so với Policy Improvement lần 1 nên thuật toán sẽ dừng lại.
Kết quả Policy trong game Pac-Man
Toàn bộ code có thể xem chi tiết tại: snowyfield1906/ai-general-research/reinforcement_learning .
Xem tại PolicyIteration.py .
def __init__ ( self , reward_function , transition_model , init_policy = None , init_value = None ) :
self . n_states = transition_model . shape [ 0 ]
self . reward_function = np . nan_to_num ( reward_function )
self . transition_model = transition_model
if init_policy is None :
self . policy = np . random . randint ( 0 , A . LEN , self . n_states )
else :
self . policy = init_policy
if init_value is None :
self . values = np . zeros ( self . n_states )
else :
self . values = init_value
def one_evaluation ( self ) :
old = self . values
new = np . zeros ( self . n_states )
# Approach 1
# for state in range(self.n_states):
# action = self.policy[state]
# probability = self.transition_model[state, action]
# reward = self.reward_function[state]
# new[state] = reward + T.DISCOUNT_FACTOR * np.inner(probability, old)
# Approach 2
A = np . eye ( self . n_states ) - T . DISCOUNT_FACTOR * self . transition_model [ range ( self . n_states ) , self . policy ]
b = self . reward_function
new = np . linalg . solve ( A , b )
self . values = new
delta = np . max ( np . abs ( old - new ) )
return delta
def evaluation ( self ) :
delta = float ( 'inf' )
delta_history = [ ]
while delta > T . STOP_CRITERION and len ( delta_history ) < T . EVALUATION_LIMIT :
delta = self . one_evaluation ( )
delta_history . append ( delta )
return len ( delta_history )
def policy_improvement ( self ) :
update_policy_count = 0
for state in range ( self . n_states ) :
temp = self . policy [ state ]
next_values = np . zeros ( A . LEN )
for action in A . ACTIONS :
probability = self . transition_model [ state , action ]
next_values [ action ] = np . inner ( probability , self . values )
self . policy [ state ] = np . argmax ( next_values )
if temp != self . policy [ state ] :
update_policy_count += 1
return update_policy_count
def train ( self ) :
delta = float ( 'inf' )
eval_history = [ ]
while delta != 0 and len ( eval_history ) < T . IMPROVEMENT_LIMIT :
sweeps = self . evaluation ( )
delta = self . policy_improvement ( )
eval_history . append ( sweeps )
Xem tại Visualizer.py .
Xem tại test-PolicyIteration.py .